Största och minsta värde i cirkelskiva x^2+y^2<=1
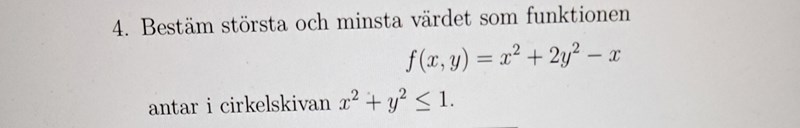
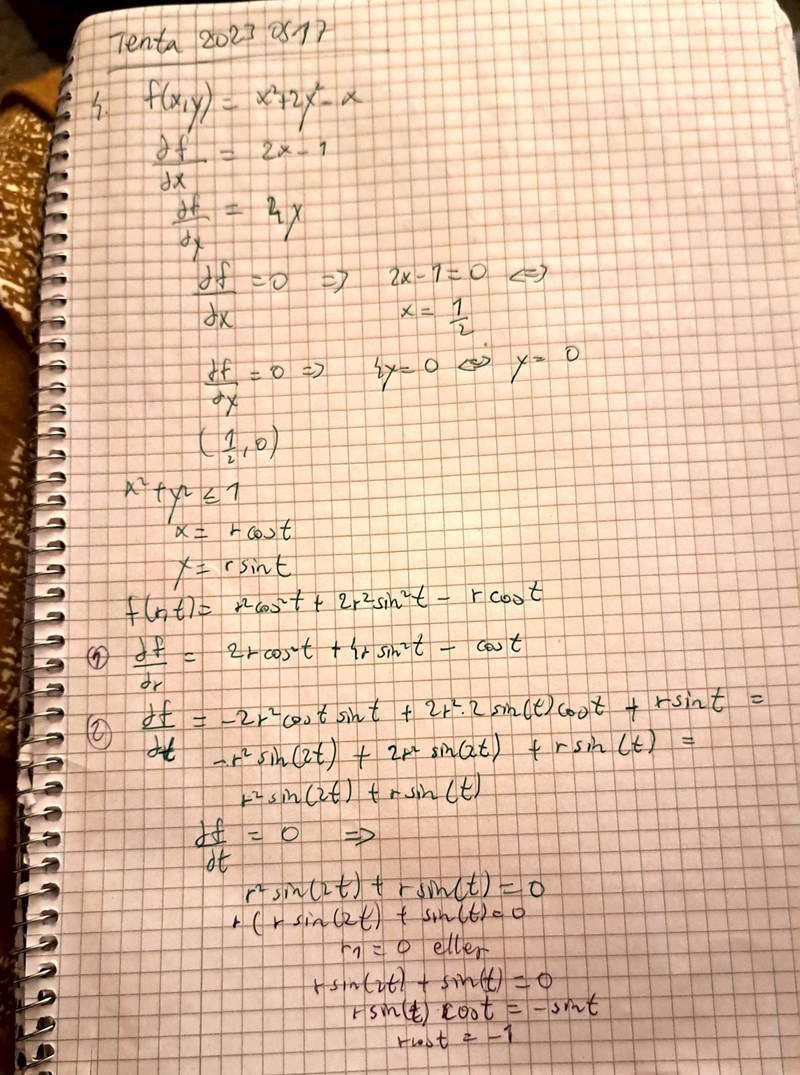 Hej!
Hej!
Det verkar bli jätterörigt med polära koordinater i denna uppgift. Ska jag testa utan det? Jag tänker mig x=t och då blir y=+-sqrt(1-t^2). Men eftersom vi tar roten ur så tillkommer +- framför rotuttrycket. Ska vi ta den positiva eller negativa?
-1.jpg?width=800&upscale=false)
Jag löste den med denna parametrisering,men får ej samma svar som facit.

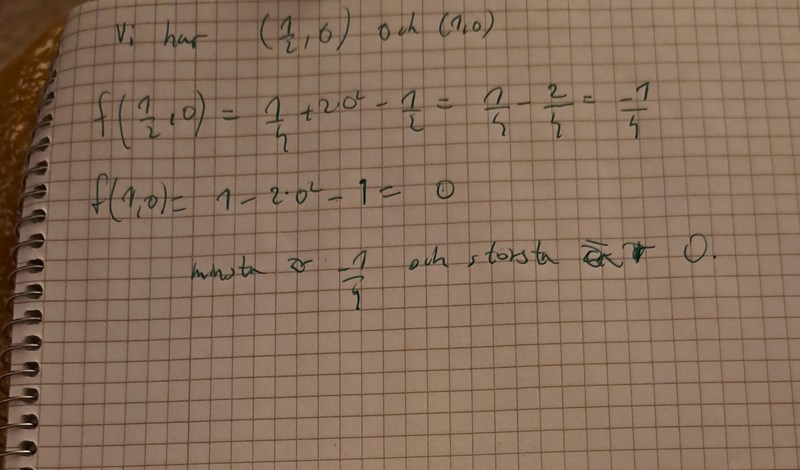
Du redovisar alldeles för lite för att det skall gå att följa med i hur du tänker. Är det stationära punkter inuti skivan du letar efter, eller undersäker du områdets rand?
Smaragdalena skrev:Du redovisar alldeles för lite för att det skall gå att följa med i hur du tänker. Är det stationära punkter inuti skivan du letar efter, eller undersäker du områdets rand?
Stationära punkter inuti skivan. Hur undersöker jag områdets rand? Jag försökte parametrisera med x=rcost och y=rsint men den metoden funkar ej alls för att lösa uppgiften. Jag får en jobbig uttryck enligt bilden ovan. Ska jag sätta r=1?
Om du skall undersöka områdets rand kan du sätta r = 1, eller utnyttja att . Jag har inte kollat vilket som verkar enklast i just det här fallet.
Smaragdalena skrev:Om du skall undersöka områdets rand kan du sätta r = 1, eller utnyttja att . Jag har inte kollat vilket som verkar enklast i just det här fallet.
Det funkade ej med y=+-sqrt(1+x^2) då jag satte x=t då facit fick att största värde är 9/4 medan jag fick det till 0. Får man fråga varför man gör på det andra sättet? Varför funkar ej x=t samt y=+-sqrt(1-t^2)?
Jag tycker cos(t) och sin(t) kunde vara lämpligt.
Trinity2 skrev:Jag tycker cos(t) och sin(t) kunde vara lämpligt.
Aa facit använde också det men jag förstår ej skälet. en annan sak de skriver ej x=rcost och y=rsint när de parametriserar utan de använder r=1. Varför gör de det?
Du har undersökt det "inre" området. Kvar återstår randen, den beskrivs av
x^2+y^2=1
Det är en enhetscirkel.
Den parameteriserar vi som
x(t) = cos(t)
y(t) = sin(t)
och ersätter x och y i funktionen
f
=x^2+2y^2-x
=x^2+y^2+y^2-x // x^2+y^2=1 på randen
=1+y^2-x
=1+sin(t)^2-cos(t)
=1+(1-cos(t)^2)-cos(t) // trig-ettan
=2-cos(t)^2-cos(t)
Nu kan man kasta sig över denna och derivera med avseende på t. Det är säkert så de gör i boken. Prova och återkom med dina räkningar, sedan kan jag lära ut ett knep om så önskas.
Trinity2 skrev:Du har undersökt det "inre" området. Kvar återstår randen, den beskrivs av
x^2+y^2=1
Det är en enhetscirkel.
Den parameteriserar vi som
x(t) = cos(t)
y(t) = sin(t)
och ersätter x och y i funktionen
f
=x^2+2y^2-x
=x^2+y^2+y^2-x // x^2+y^2=1 på randen
=1+y^2-x
=1+sin(t)^2-cos(t)
=1+(1-cos(t)^2)-cos(t) // trig-ettan
=2-cos(t)^2-cos(t)
Nu kan man kasta sig över denna och derivera med avseende på t. Det är säkert så de gör i boken. Prova och återkom med dina räkningar, sedan kan jag lära ut ett knep om så önskas.
Yes så gör de i facit. Men då ska jag undvika att parametrisera med x=rcost och y=rsint eftersom r=1 ligger på randen. Jag vet att vid dubbelintegraler brukar man skriva x=rcost och y=rsint och sen är randen i ett givet intervall
Ja, i det härfallet är r=1 eftersom det är ekvationen
x^2+y^2=1
HL är r^2 i den allmänna cirkelformen
x^2+y^2=r^2. = cirkel med radien r
Här har du alltså r=1
Hade området varit
x^2+y^2=4
hade du använt r=2 och haft
x=2cos(t)
y=2sin(t)
Trinity2 skrev:Ja, i det härfallet är r=1 eftersom det är ekvationen
x^2+y^2=1
HL är r^2 i den allmänna cirkelformen
x^2+y^2=r^2. = cirkel med radien r
Här har du alltså r=1
Hade området varit
x^2+y^2=4
hade du använt r=2 och haft
x=2cos(t)
y=2sin(t)
Ja men hur hade det varit om vi skulle haft x^2+y^2<1 ? Då kan man ju ej skriva x= cost och y=sint
Det området har ingen rand. Det har bara "ett inre" som du undersöker med stationära punkter.
Jämför med y=x på intervallet [0,1)
Vad är minsta och vad är största värde för y?
Trinity2 skrev:Det området har ingen rand. Det har bara "ett inre" som du undersöker med stationära punkter.
Jämför med y=x på intervallet [0,1)
Vad är minsta och vad är största värde för y?
Aa okej största saknas för 1 ingår ej. Minsta är 0
destiny99 skrev:Trinity2 skrev:Det området har ingen rand. Det har bara "ett inre" som du undersöker med stationära punkter.
Jämför med y=x på intervallet [0,1)
Vad är minsta och vad är största värde för y?
Aa okej största saknas för 1 ingår ej. Minsta är 0
Rätt. Det blir samma sak på ett öppet område som x^2+y^2<1, det är i 2 dimensioner istället för 1.
Sedan kan det finnas ett max i området, det beror på f, men randen ingår ej iaf.
Antag nu att det finns en topp (max) i det inre. Då kan man fråga sig "Om vi inte randen är med, vad händer nära randen? Kan det vara så att f överstiger max nära randen?"
Vad man gör i dessa fall är att man skriver
x=r cos(t)
y=r sin(t)
och så undersöker man hur f beter sig när r->1 i olika riktningar t. Kanske det kommer en sådan uppgift längre fram i din bok.
Trinity2 skrev:destiny99 skrev:Trinity2 skrev:Det området har ingen rand. Det har bara "ett inre" som du undersöker med stationära punkter.
Jämför med y=x på intervallet [0,1)
Vad är minsta och vad är största värde för y?
Aa okej största saknas för 1 ingår ej. Minsta är 0
Rätt. Det blir samma sak på ett öppet område som x^2+y^2<1, det är i 2 dimensioner istället för 1.
Sedan kan det finnas ett max i området, det beror på f, men randen ingår ej iaf.
Antag nu att det finns en topp (max) i det inre. Då kan man fråga sig "Om vi inte randen är med, vad händer nära randen? Kan det vara så att f överstiger max nära randen?"
Vad man gör i dessa fall är att man skriver
x=r cos(t)
y=r sin(t)
och så undersöker man hur f beter sig när r->1 i olika riktningar t. Kanske det kommer en sådan uppgift längre fram i din bok.
Aa jag har ej stött på en sån uppgift eller sett i pdf än. Jag ville bara veta hur man ska tänka i en sån situation


