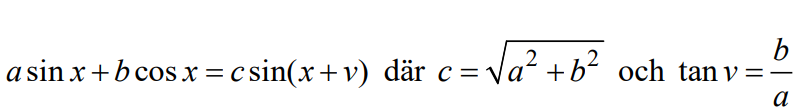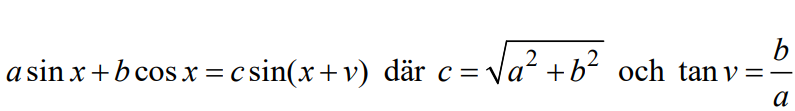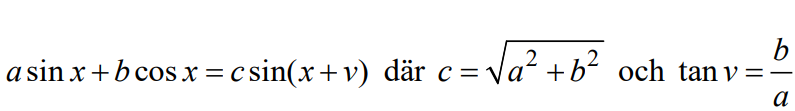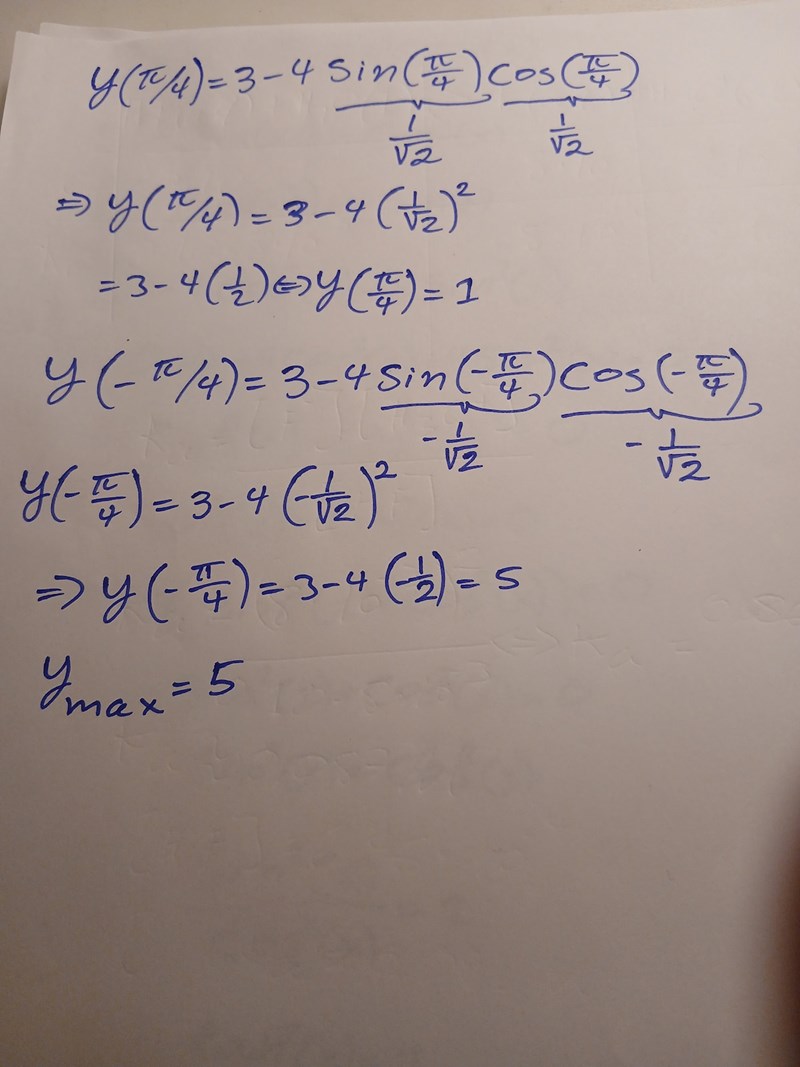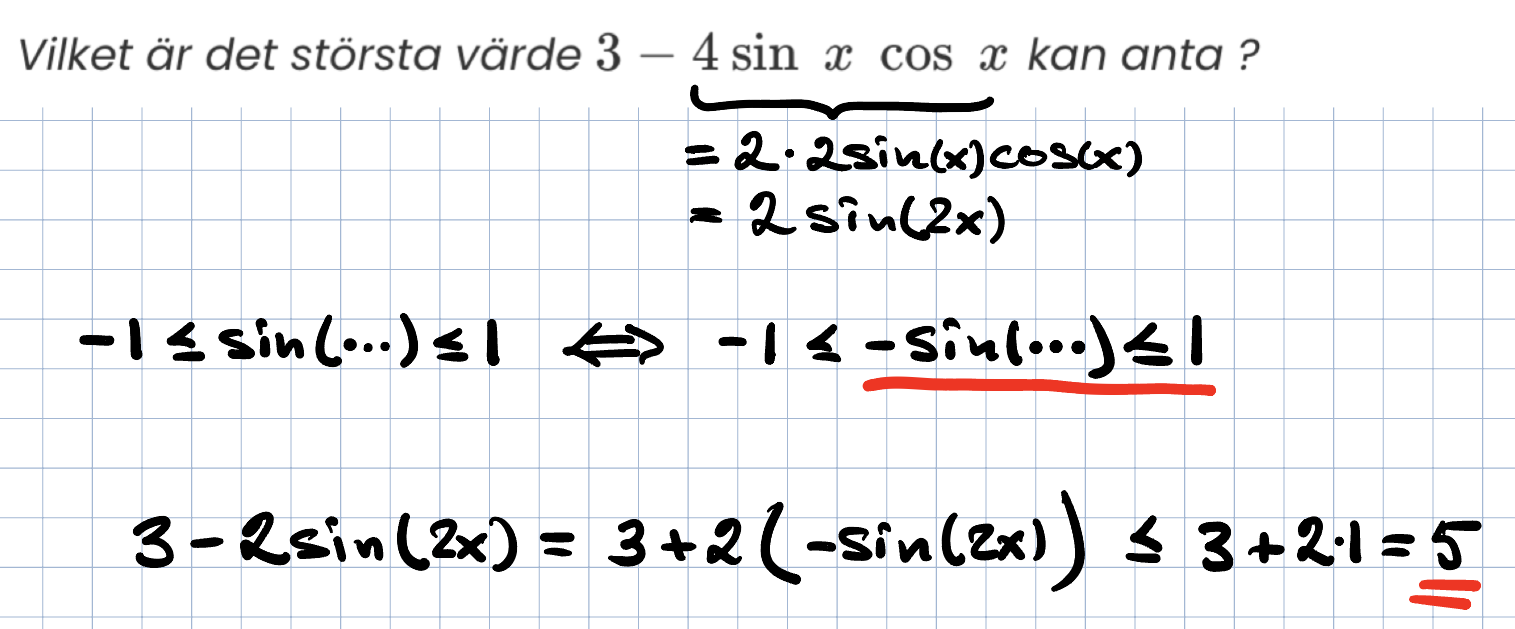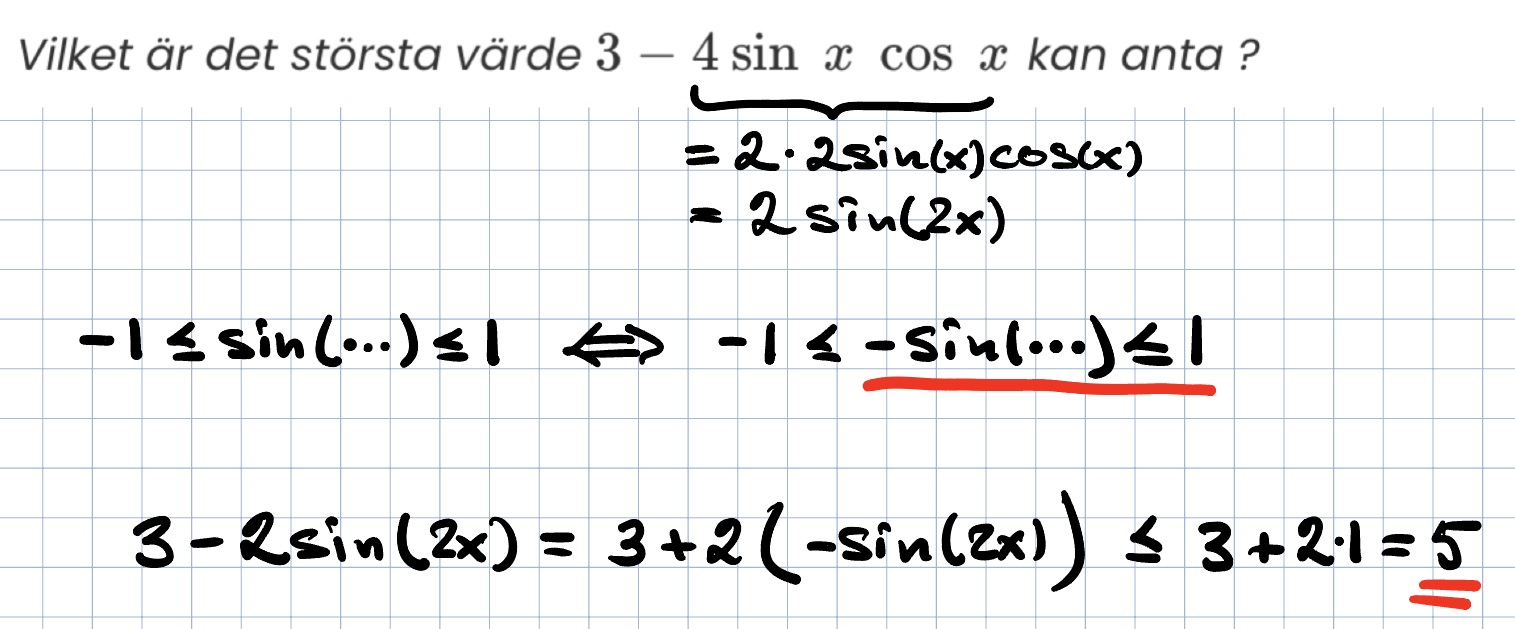Största värdet som Trig funktionen antar

Är det en bra ansats att tillämpa den här formeln?

För att hitta maxvärdet

sin(x)=1

gäller sambandet även så att sin(2x)=1 ?

Arup skrev:

För att hitta maxvärdet

sin(x)=1

gäller sambandet även så att sin(2x)=1 ?

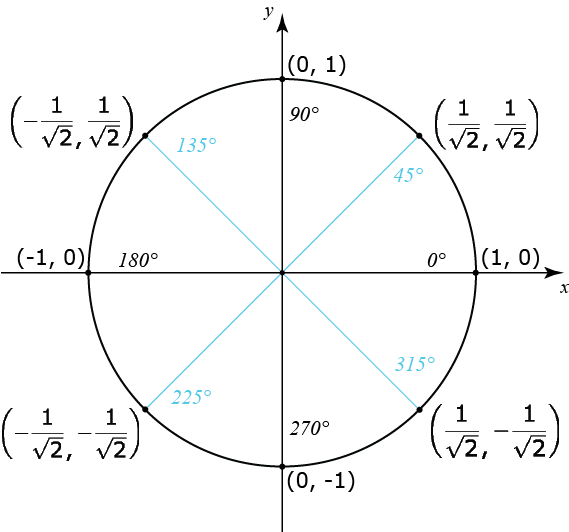
Nej, när sin(x)=1 är inte sin(2x)=1. Då är sin(2x)=0. Se enhetscirkeln. Däremot blir sin(2x) aldrig >1.

Jag skulle tänka så här:

För att uttrycket skall bli så stort som möjligt måste den andra termen $4\sin \left(x\right)\cos \left(x\right)$ vara så liten som möjligt. Den får gärna vara negativ.

Kika på enhetscirkeln igen. Vid 0, 90, 180, 270 grader är antingen cos eller sin =0. Det gör att produkten blir =0.

Men precis mitt emellan dessa gradtal blir produkten av sin och cos så stor som möjligt, om man bara tänker på absolutbeloppet (utan minustecken alltså).

Jag vet ju att du gillar formler, så då kan du ju ta till "dubbla vinkeln" istället: $\sin \left(2x\right)=2\sin \left(x\right)\cos \left(x\right)$

Själv tycker jag enhetscirkeln är bra att plocka fram då och då, för att förstå hur saker hänger samman.

så menar du alltså någon funktionerna ska vara -1 ?

tex sin(x)=-1 eller cos(x)=-1 ?

Arup skrev:

Är det en bra ansats att tillämpa den här formeln?

Prova.

Laguna skrev:

Arup skrev:

Är det en bra ansats att tillämpa den här formeln?

Prova.

Hur hjälper det här mig att få fram det maximala värdet på funktionen?

Arup skrev:

så menar du alltså någon funktionerna ska vara -1 ?

tex sin(x)=-1 eller cos(x)=-1 ?

Nej, det menar jag inte.

Om sin(x)=-1 så är cos(x)=0.

Om cos(x)=-1 så är sin(x)=0.

I både fallen är produkten noll. Titta på enhetscirkeln!

Om däremot exempelvis cos(x)<0 och sin(x)>0 så blir produkten negativ. Det är den du behöver komma fram till hur du hittar. Här kan enhetscirkeln hjälpa igen. 

Alternativt använder du "dubbla vinkeln" jag tipsade om.

Läs mitt svar #5 en gång till och fundera.

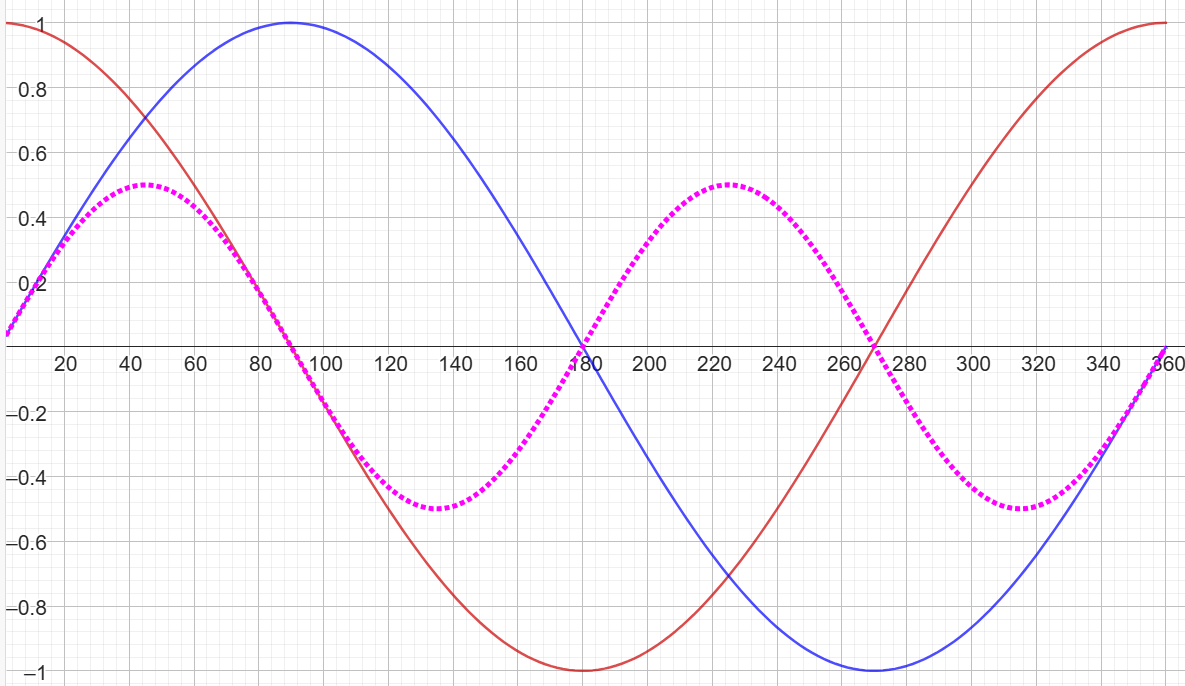
Bjuder på hur sin(x) i rött, samt cos(x) i blått ser ut i intervallet 0-360 grader. Det har du sett en massa gånger. Kika även på den lila kurvan som är produkten.

Arup skrev:

Laguna skrev:

Visa föregående citat

Arup skrev:

Är det en bra ansats att tillämpa den här formeln?

Prova.

Hur hjälper det här mig att få fram det maximala värdet på funktionen?

Det vet jag inte om den gör. Spontant tror jag inte det. Den liknar ju inte sin(x)cos(x) alls.

Du plockade fram formeln. Laguna säger "prova", vilket är en bra uppmaning.

Prova och se om den hjälper dig att lösa problemet. 

Arup skrev:

 

Här 

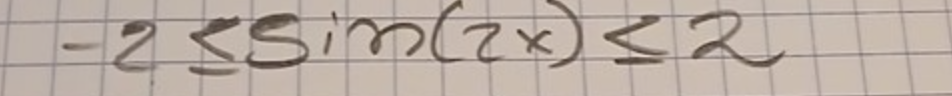
saknar jag en 2:a

En petig lärare kommer ge adrag.

Sedan är det inte likhet på slutet

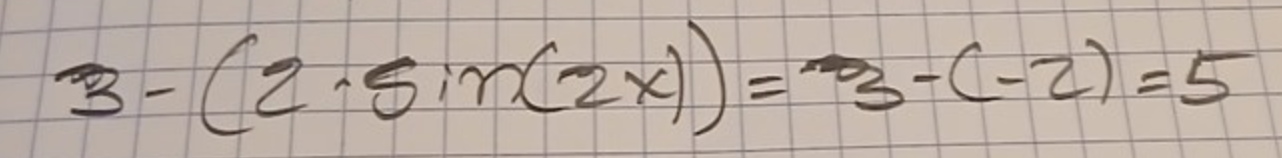
Jag vet art det var ett tag aedan jag postade denna tråd. Men skulle man kunna lösa uppgiften mha produktregeln ?

Arup skrev:

Jag vet art det var ett tag aedan jag postade denna tråd. Men skulle man kunna lösa uppgiften mha produktregeln ?

Bra spaning!

Pröva så får du se om du får fram samma resultat den vägen.

Yngve skrev:

Arup skrev:

Jag vet art det var ett tag aedan jag postade denna tråd. Men skulle man kunna lösa uppgiften mha produktregeln ?

Bra spaning!

Pröva så får du se om du får fram samma resultat den vägen.

Så här får jag det till

Det ser bra ut, förutom en liten miss på fjärde raden från slutet, där du skriver att $\cos(-\frac{\pi}{4})=-\frac{1}{\sqrt{2}}$.

Kommentar: En enklare väg från ekvationen 4(sin²(x)-cos²(x)) = 0 är att använda konjugatregeln, vilket ger dig 4(sin(x)+cos(x))(sin(x)-cos(x)) = 0.

Nollproduktmetoden ger dig då de båda ekvtionerna

• $\sin(x)+\cos(x) = 0$, med lösningar $x=-\frac{\pi}{4}+n\cdot\pi$
• $\sin(x)-\cos(x) = 0$, med lösningar $x=\frac{\pi}{4}+n\cdot\pi$

Jag undrar skulle man kunna skriva $\cos \left(x\right)$till $\sin (90-x)$?

så att funktionen blir så här $y=3-4\sin \left(x\right)\sin (90-x)$

Javisst, det går bra. Du kan sktäriva om ekvationen hur du vill, så länge du använder matematiska identiteter.

Om jag snabbt vill bilda mig en uppfattning skulle jag använda enhetscirkeln. För övrigt är det bra att vara välbekant med den. 

(sin x)(cos x) är arean av den rektangel som bildas mellan origo och punkten på cirkeln. 

En kvadrat är den rektangel som har störst area givet omkretsen. Då är sin och cos båda 1/√2, med varierande tecken. Alltså är uttrycket som störst/minst +/- 1/2. 

4*(-1/2)=-2 och 3-(-2)=5 

sictransit skrev:

Om jag snabbt vill bilda mig en uppfattning skulle jag använda enhetscirkeln. För övrigt är det bra att vara välbekant med den. 

(sin x)(cos x) är arean av den rektangel som bildas mellan origo och punkten på cirkeln. 

En kvadrat är den rektangel som har störst area givet omkretsen. Då är sin och cos båda 1/√2, med varierande tecken. Alltså är uttrycket som störst/minst +/- 1/2. 

4*(-1/2)=-2 och 3-(-2)=5 

Hur kan det ha varierande tecken de båda koordinaterna ligger ju väl på den 1:a kvadranten ?

Arup skrev:

sictransit skrev:

Om jag snabbt vill bilda mig en uppfattning skulle jag använda enhetscirkeln. För övrigt är det bra att vara välbekant med den. 

(sin x)(cos x) är arean av den rektangel som bildas mellan origo och punkten på cirkeln. 

En kvadrat är den rektangel som har störst area givet omkretsen. Då är sin och cos båda 1/√2, med varierande tecken. Alltså är uttrycket som störst/minst +/- 1/2. 

4*(-1/2)=-2 och 3-(-2)=5 

Hur kan det ha varierande tecken de båda koordinaterna ligger ju väl på den 1:a kvadranten ?

Nej, varför skulle vi bara röra oss i 1:a kvadranten? Uppgiften ger inga begränsningar av x. 

Jag förstod inte det röda (sista raden i #20)

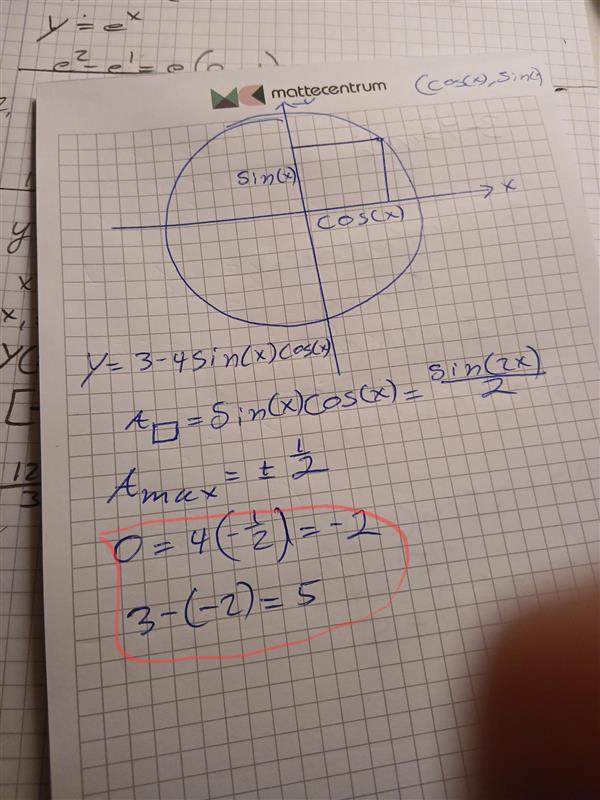
Funktionen kan skrivas

y=3-2sin(2x)

Vi har alltid: -1 ≤ sin(...) ≤ 1. ±1 är "extremvärdena" för sin(...)

Om sin(...) = -1 är y=3-2(-1)=5

Om sin(...) = +1 är y=3-2(+1)=1

Alltså kan y anta alla värden mellan 1 och 5: 1 ≤ y ≤ 5.

y(-1) = 3-2sin(-2) och inte det du skriver

Skriv

y_max = 3-2(-1) = 5

Samma sak med y(1)

kommer du ihåg denna lösning för ett tag sen ?

Arup skrev:

kommer du ihåg denna lösning för ett tag sen ?

Bild syns ej

Arup skrev:

Ja