Största volym på kon (Matematik/Matte 5)

Radien r får du betrakta som en given konstant, ty annars kan du får hur stor volym på konen som helst bara genom att välja r tillräckligt stort. Det är medelpunktsvinkeln i cirkelsektorn som är din variabel och som kan ha ett värde för maximal volym för det givna värdet på r. Du har således inte två variabler att derivera. Lite knegig derivata bara.

Du menar r₂ ?

Ser inte riktigt vad du skrivit i fig, men det är cirkelsektorns radie (i texten angiven som r) som du får betrakta som en given konstant. Ditt r₂ är väl bottenytans radie och den beror på r och på den variabla medelpunktvinkeln.

Men hur ska man få ett numeriskt värde när V´( $α$ ) = 0? Även om man betraktar radien som en konstant? Den finns ju fortfarande kvar i uttrycket.

Förmodar att alfa är din medelpunktsvinkel. Den givna radien r får du ha med i svaret. Däremot måste du hitta det värde på alfa som ger störst volym och bestämma denna volym för detta alfa-värde.

Om uttrycket är korrekt ska radien gå att bryta ut, så att du får en faktor $r^3$ .

Jepp! Så blev det för mig också. Denna faktor kan alltså tack och lov sättas utanför derivationen (derivatans linjäritet).

Jag fick volymen :

$V = \frac{π}{3} \sqrt{\frac{2 π - {αr}_{1}}{π}} * \sqrt{\frac{{r^{2}}_{1} - 2 π - {αr}_{1}}{π}}$

Och dess derivata:

$V' (α) = - \frac{\frac{π}{3} \sqrt{2 - \frac{α r_{1}}{π}}}{2 \sqrt{{r^{2}}_{1} - 2 - \frac{r_{1} α}{π}}} - \frac{r_{1} \sqrt{{r^{2}}_{1} - 2 - \frac{r_{1} α}{π}}}{6 \sqrt{2 - \frac{α r_{1}}{π}}}$

DuckD25 skrev:
Jag fick volymen :

$V = \frac{π}{3} \sqrt{\frac{2 π - {αr}_{1}}{π}} * \sqrt{\frac{{r^{2}}_{1} - 2 π - {αr}_{1}}{π}}$

Och dess derivata:

$V' (α) = - \frac{\frac{π}{3} \sqrt{2 - \frac{α r_{1}}{π}}}{2 \sqrt{{r^{2}}_{1} - 2 - \frac{r_{1} α}{π}}} - \frac{r_{1} \sqrt{{r^{2}}_{1} - 2 - \frac{r_{1} α}{π}}}{6 \sqrt{2 - \frac{α r_{1}}{π}}}$

Det ser inte ut att stämma. Du kan få negativa värden i rotuttrycken, vilket betyder att volymen inte är definierad för alla r>0.

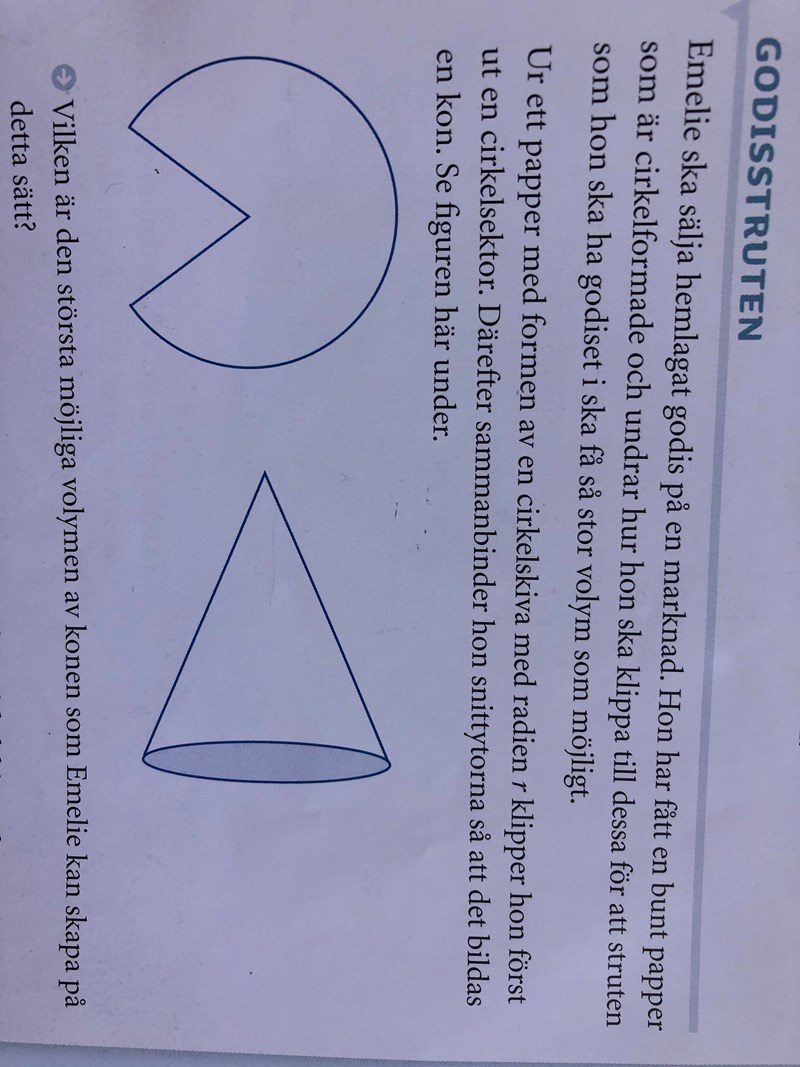
Du borde kunna klippa ut en bit ur en cirkelskiva med vilken radie som helst för att göra en kon.

Om vi är överens om att konens basytas radie är $r_{K} = r_{C} (1 - \frac{α}{2 π})$ , kan du t.ex förenkla uttrycket genom att låta $(1 - \frac{α}{2 π}) = k$ .

Radien blir då istället $r_{K} = r_{C} k$ och höjden $h_{K} = \sqrt{{r^{2}}_{C} - {r^{2}}_{C} k^{2}} = r_{C} \sqrt{1 - k^{2}}$ .

Volymfunktionen, en funktion av k, blir mycket mer kompakt och derivatan blir inte alls lika knölig att utvärdera. Hoppas det var begripligt.

Det var så jag löste det i alla fall. Ni andra i tråden får stoppa mig om jag är fel ute.

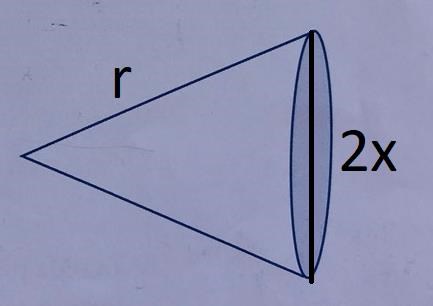
Du borde kunna tänka så här. Vilken är den största volymen av en kon med dimensioner enligt nedan:

$V (x) = \frac{π x^{2} \sqrt{r^{2} - x^{2}}}{3}$

Eftersom alla möjliga bottenradier (0<x<r) kan man få till genom att klippa papperet.

Jag har samma uppgift, och tänkte själv på följande vis:

(R är radien på cirkeln, alltså konens sida vilken är konstant, r är konens radie och h är konens höjd)

Pyt. ger att R²=r²+h²

Vi kan skriva om det till:

r²=R²-h² vilket är smidigt, då det finns ett r² i den allmänna formeln för koners volym.

Då kan vi skriva följande formel:

$v (h) = \frac{πh (R^{2} - h^{2})}{3}$ $= \frac{{πhR}^{2}}{3} - \frac{{πh}^{3}}{3}$

Derivat kan ge min/max-punkt om den är lika med 0, så vi får följande ekvation:

$v' (h) = \frac{{πR}^{2}}{3} - {πR}^{2} = 0$

viket efter förenkling ger:

$\pm \frac{R}{\sqrt{3}} = h$

vi vet att endast det positiva stämmer, finns inga negativa mått, plus att vi kan gissa vilken form den negativa 3-gradsformeln har.

Vi kan stoppa in $\frac{R}{\sqrt{3}}$ i formeln för volymen och sedan se vad vi får.( $v_{m a x} =$ $\frac{π \frac{R}{\sqrt{3}} (R^{2} - {(\frac{R}{\sqrt{3}})}^{2})}{3}$ )

Detta ger att $v_{m a x} = \frac{2 π}{\sqrt{243}} R^{3}$

Tror detta är rätt i alla fall...