Summa
Hej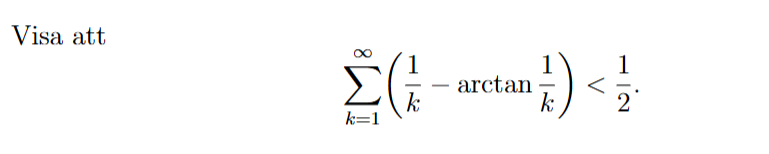
Jag har börjat med att skriva om det som står inom parantesen till .
Man kanske kan använda serieutvecklingen av arctan.
Man kan också jämföra den givna summan med en integral. (se bevis till integralkriteriet för konvergens av serier)
, där är en avtagande positiv funktion (då x>0).
Därmed gäller att
Det återstår att beräkna
, vilket verkligen är mindre än 1/2 eftersom .
Jag håller på med beräkningen av integralen f(x) = 1/x -arctan(1/x). Efter ett par försök har jag funnit primitiven ln(x/sqrt(x^2 +1)) -xarctan(1/x).
Min fråga är nu hur gör man med xarctan(1/x) då x går mot INF? Är det nu man tillämpar Maclaurin?
Maclaurin funkar utmärkt.
Alternativt kan man göra variabelbyte i gränsvärdet och sedan utnyttja definitionen av derivatan:
EDIT: Gränsvärdet (arctan t) / t då t->0 finns ibland (d.v.s. beroende på kurslitteratur) med på listan över "standardgränsvärdena".
Det där var fiffgt, jag skulle dock aldrig kunna komma på det på egen hand..
Hursomhelst närmar sig xarctan(1/x) 1 då x -> INF. Jag satt in rätt siffror på rätt plats för den formeln med jämförelse av summor & integraler och har slutligen kommit fram till att
Jag skrev om det med lite logaritmlagar och fick äntligen samma svar som du skrev tidigare.. Tack för hjälpen!
Undrar dock hur man kan motivera val av metod på en tenta. Alltså den formeln för jämförelse av integraler/summor; typ rita en figur?
Figur passar jättebra som motivering för jämförelsen mellan summan och integralen.
- integralen tolkas som arean mellan funktionskurvan och x-axeln,
- summan från 1 till INF tolkas som totala arean av övertrappan som består av staplar med bredd = 1.
- summan från 2 till INF blir då arean av undertrappan som består av staplar med bredd = 1.
Notera också att man måste motivera på något sätt att f(x)= 1/x - arctan 1/x är avtagande och positiv för att få utnyttja sambandet mellan summor och integraler
Ja vad bra det var precis så jag tänkte! Och det med strängt avtagande kan man motivera genom att derivera och visa derivatan är negativ för typ x>0


