Summa av fourieserie

Hej, enligt konvergenssatsen konvergerar ju fourierserien F(a) mot funktionens f(a) om f är kontinuerlig i punkten x = a. Enligt uppgiftsbeskrivningen verkar ju f(x) vara kontinuerlig i punkten x = π. Så varför beräknar facit högergränsvärdet? Borde man inte enbart beräkna vänstergränsvärdet i x = -π eftersom funktionen f(x) inte är kontinuerlig där? Varför beräknar de även högergränsvärdet där x = π?

Uppgiften:

Facit:

Rita grafen för funktionen $f$ i enlighet med uppgiften! Då kommer du se att funktionen har en språngdiskontinuitet i punkterna $\pi + n\cdot 2\pi$ .

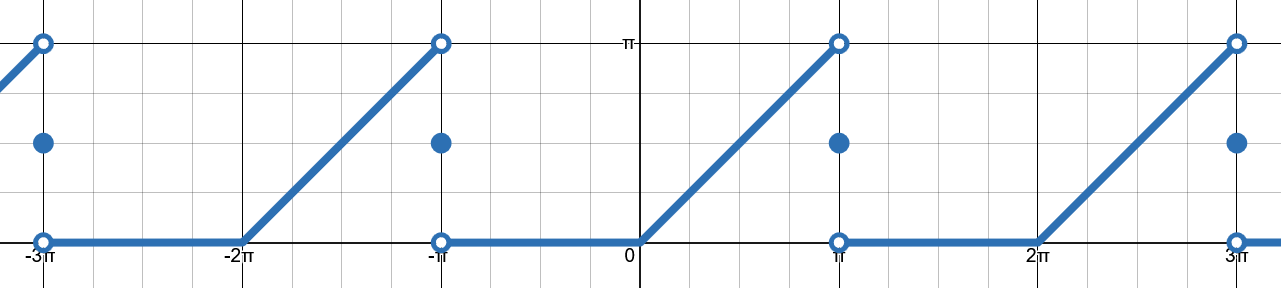
Grafen är ju:

en vågrät sträcka y=0 för x mellan -pi och 0
en sned sträcka y=x (med 45-graders lutning) för x mellan 0 och pi

Dessa två sträckor sedan "kopieras och klistras" förskjutna med heltalsmultiplar av perioden 2pi.

Visa spoiler

Svara