Summa och produkt av komplexa rötter (Matematik/Universitet)

Alla ekvationer kan skrivas som (z-rot1)(z-rot2)... Börja med egna andragradare eller tredjegradare osv och se vad som händer. Välj enkla tal och räkna ut innan vad du letar efter.

Som Micimacko skriver, så går din ekvation att skriva som

(z-rot1)*(z-rot2)*(z-rot3)*(z-rot4)*(z-rot5)*(z-rot6)*(z-rot7) = 0

Vi vet inte värdena på de sju rötterna, men vi vet att ekvationen kan skrivas så. Produkten av alla de där faktorerna blir noll då, och enbart då, någon av parenteserna är noll.

Det är inte jätteenkelt att multiplicera ihop parenteserna, men det går. Det blir 196 termer att addera ihop. En enda av de termerna innehåller z^7, och en enda av de termerna innehåller z^0 (dvs enbart konstanterna rot1, rot2, ...) i någon kombination.

Vad är den termen som innehåller z^7 ?

Vad är den termen som enbart innehåller konstanter?

$z^7=z^7\cdot 1$

Bubo, jag antar att du menar $z^{6}$ -termen?

tomast80 skrev:
$z^7=z^7\cdot 1$
Bubo, jag antar att du menar $z^{6}$ -termen?

Nej, men jag tänkte komma dit efter de bägge enklaste termerna. :-)

Bubo skrev:
Vad är den termen som innehåller z^7 ?
Vad är den termen som enbart innehåller konstanter?

Jag vet inte riktigt hur jag ska göra detta, binomialsatsen funkar ju bara på binom. Man skulle ju kunna multiplicera in alla faktorerna, men det blir väldigt mycket arbete. Finns det något lättare sätt?

Termen som innehåller z^7 borde dock vara 1 eftersom att man bara väljer z och Inga andra termer.

Termen som innehåller enbart konstanter borde vara rot1*rot2*…*rot7, men jag vet ju inte rötterna

Porkshop skrev:
Bubo skrev:
Vad är den termen som innehåller z^7 ?
Vad är den termen som enbart innehåller konstanter?
Jag vet inte riktigt hur jag ska göra detta, binomialsatsen funkar ju bara på binom. Man skulle ju kunna multiplicera in alla faktorerna, men det blir väldigt mycket arbete. Finns det något lättare sätt?
Termen som innehåller z^7 borde dock vara 1 eftersom att man bara väljer z och Inga andra termer.
Termen som innehåller enbart konstanter borde vara rot1*rot2*…*rot7, men jag vet ju inte rötterna

Vet du produkten av dem?

Jag vet att koefficienten framför z^6 termen är (3-i)

Så någon kombination av termer från (z-rot1)*(z-rot2)*(z-rot3)*(z-rot4)*(z-rot5)*(z-rot6)*(z-rot7) ska bli z^6

Sen kan jag väll sätta likheten att denna product är lika med (3-i) och att koefficienten framför z^3 är π

Koefficienten framför Z^0 är också e

Så -rot1*-rot2*-rot3*…*-rot7 = e

Jag ser att koefficienten framför z^6 är (3-i) men I faktorform kan det ju antingen vara z^6*rot1 , z^6*rot2 osv.

Hur ska jag härleda en ekvation för att lösa ut koefficienterna på ett enkelt sätt utan att behöva multiplicera ihop alla termerna?

Jag får verkligen inte till det...

Det enda jag kommit fram till är att (-rot1)*(-rot2)*…*(-rot7) = e $\Leftrightarrow$ (rot1)*(rot2)…*(rot7) = -e

Men jag vet inte hur jag ska gå vidare med summan av rötterna.

Jag läser uppgiftens första mening. Behöver man leta efter alla sju rötterna för att lösa uppgiften?

Exempel: Summera sju vektorer i det imaginära planet och den sista (sjunde) vektorn pekar väl på reala- ( x-) axeln med värdet "-e"?

Jag vet egentligen inte svaret, men har en ganska stark känsla av att de andras svamlande om z^6 där uppe betyder nånting. Har du testat att utveckla en likadan av lägre grad för att se?

Jag har testat mig fram på polynom av lägre grad, men kan inte lista ut vad jag letar efter.

Det där med summan av 7 vektorer med sista på -e är precis så jag tänkt, men jag kan inte komma på hur man ska få reda på vilka det är...

Porkshop skrev:
Jag har testat mig fram på polynom av lägre grad, men kan inte lista ut vad jag letar efter.
Det där med summan av 7 vektorer med sista på -e är precis så jag tänkt, men jag kan inte komma på hur man ska få reda på vilka det är...

Gå tillbaks till den ursprungliga frågan, vad exakt är de ute efter?

Härledning för polynom av grad 2:

$x^2+px+q=0$

$(x-x_1)(x-x_2)=x^2-x\cdot x_1-x\cdot x_2+x_1\cdot x_2=$

$x^2-(x_1+x_2)x+x_1x_2=x^2+px+q\Rightarrow$

$x_1+x_2=-p$

$x_{1} x_{2} = q$

Justdet, jag fattar nu vad du går efter och hur jag ska härleda ekvationen. Men att multiplicera ihop alla binom blir väldigt jobbigt, finns det något effektivare sätt?

Induktionsbevis, kanske?

Hur menar du? Jag har verkligen ingen aning.

Men det går ju att bryta ut z^3 ur ekvationen vilket innebär att vi har en trippelrot i z=0 så produkten av samtliga rötter blir enkel.

Detta lämnar oss med ett fjärdegradspolynom att undersöka vilket ger lite lättare beräkningar. Är det dessutom inte så att komplexa rötter till ett polynom är parvis varandras komplexkonjugat? Det ger oss fler ledtrådar.

Jo, men jag kan inte bryta ut z^3 från e

Jag kan inte heller se att noll skulle vara en rot. Jag testade såhär, du kan bara strunta i allt småkraffs om vi tittar på z^6, för det kommer aldrig upp i så hög grad ändå, så går det ganska fort att bara ta bort parenteserna.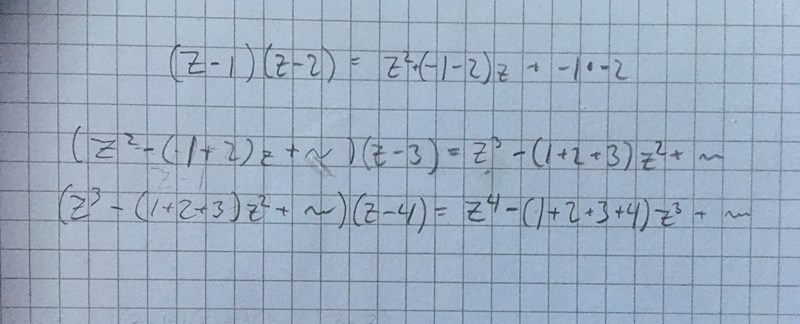

Usch vad slarvigt av mig, jag missade den termen. Så produkten blir inte 0.

Då gäller det att vi får 1, 3 eller 5 reella rötter och 6, 4 eller 2 komplexa rötter som är parvis varandras komplexkonjugat. ( det kan inte bli 7 reella rötter då vi har komplexa faktorer) detta innebär att både summan och produkten kommer att bli reella tal.

Är det inte så att produkten kan vi läsa ut direkt med tanke på vad Tomast80 och Affe jpg sagt ovan?

Ja men så är det ju. Därmed är -(1+2+3+4+5+6+7) = 3-i $\Leftrightarrow$ (1+2+3+4+5+6+7) = -3 + i vilket är svaret.

Då löste jag uppgiften såhär:

$a) w = z^{7} + (3 - i) z^{6} + πz + e = 0 = (z - z_{1}) (z - z_{2}) (z - z_{3}) (z - z_{4}) (z - z_{5}) (z - z_{6}) (z - z_{7}) \Rightarrow e = (- z_{1}) (- z_{2}) (- z_{3}) (- z_{4}) (- z_{5}) (- z_{6}) (- z_{7}) \Leftrightarrow z_{1} z_{2} z_{3} z_{4} z_{5} z_{6} z_{7} = - e b) (z - z_{1}) (z - z_{2}) = z^{2} - (z_{1} + z_{2}) z + a_{1} Där a_{n} är irrelevanta konstaner eller variabler . (z^{2} - (z_{1} + z_{2}) z + a) (z - z_{3}) = Z^{3} - (z_{1} + z_{2} + z_{3}) z^{2} + a_{2} \Rightarrow \Rightarrow w = z^{7} - (z_{1} + z_{2} + z_{3} + z_{4} + z_{5} + z_{6} + z_{7}) z^{6} + a_{7} \Rightarrow - (z_{1} + z_{2} + z_{3} + z_{4} + z_{5} + z_{6} + z_{7}) = 3 + i \Leftrightarrow z_{1} + z_{2} + z_{3} + z_{4} + z_{5} + z_{6} + z_{7} = - 3 + i$

Tack för all hjälp allihop!

Men hur skulle jag kunna gå till väga för att lösa hela ekvationen eller måste man gissa nollställen?

Och skulle ni löst uppgiften på ett annat sätt? Jag vill gärna ha många metoder i förrådet :)

Edit:

Oj, det blev inte så snyggt formerat. Jag vet inte hur jag fixar...

AndersW skrev:
Men det går ju att bryta ut z^3 ur ekvationen vilket innebär att vi har en trippelrot i z=0 så produkten av samtliga rötter blir enkel.
Detta lämnar oss med ett fjärdegradspolynom att undersöka vilket ger lite lättare beräkningar. Är det dessutom inte så att komplexa rötter till ett polynom är parvis varandras komplexkonjugat? Det ger oss fler ledtrådar.

Rötterna är varandras konjugat bara om polynomet har reella koefficienter. I övriga fall kan man ju alltid ta godtyckliga komplexa tal och göra ett polynom, t.ex (z-2i)(z+3i).

För att hitta rötterna måste man troligen använda numeriska metoder. De har nog bara kastat in lite roliga tal som koefficienter här eftersom vi inte behöver hitta rötterna.

Note to self: Två koppar kaffe innan du börjar svara på pluggakuten. :)

Förslag på lösning nedan:

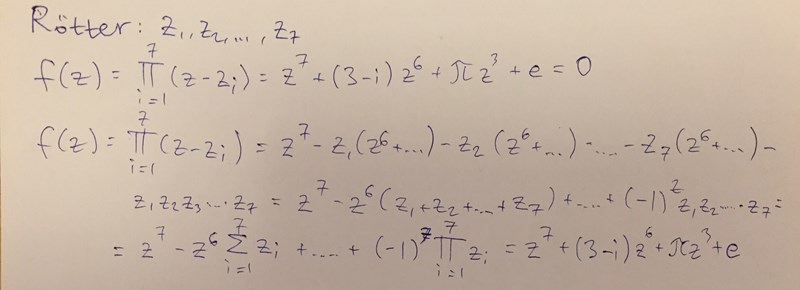
Jag tog reda på alla rötterna, och de är fördelade lite roligt: en på ungefär -3+i och de övriga i tre par som nästan är varandras konjugat precis innanför enhetscirkeln.

Hur tog du reda på dem?

Micimacko skrev:
Hur tog du reda på dem?

Skrev ett litet program, alltså ren numerisk behandling, med Newton-Raphsons metod. Men det finns förmodligen webbsidor som gör hela jobbet, t.ex. wolfram och sånt.

Micimacko skrev:
Hur tog du reda på dem?

Gissningsvis via Wolfram Alpha e.d.:

https://www.wolframalpha.com/input/?i=z%5E7%2B(3-i)z%5E6+%2B+%CF%80z%5E3%2Be%3D0

Lösningen till detta ges rakt av med Vietas formler som säger att för ett polynom av grad $n$ :

$a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0$

(där $a_n\neq0$ )

är summan av dess rötter $x_1,x_2,...,x_{n-1},x_n$ :

$\displaystyle\sum_{i=1}^nx_i=-\dfrac{a_{n-1}}{a_n}$

och produkten:

$\displaystyle\prod_{i=1}^nx_i=\left(-1\right)^n\dfrac{a_0}{a_n}$

I vårt fall är $n=7,a_n=1$ , $a_{n-1}=3-i$ och $a_0=e$ vilket ger att summan av rötterna är $-3+i$ och produkten $-e$ .