Svängande pendel

Pendeln svänger kring z-axeln och du ska beräkna den högsta vinkelhastigheten för pendel B som har höjden L = 0,587 m och bredden a = 0,493 m om svängningsamplituden är 90,0 ·10^-3 rad.

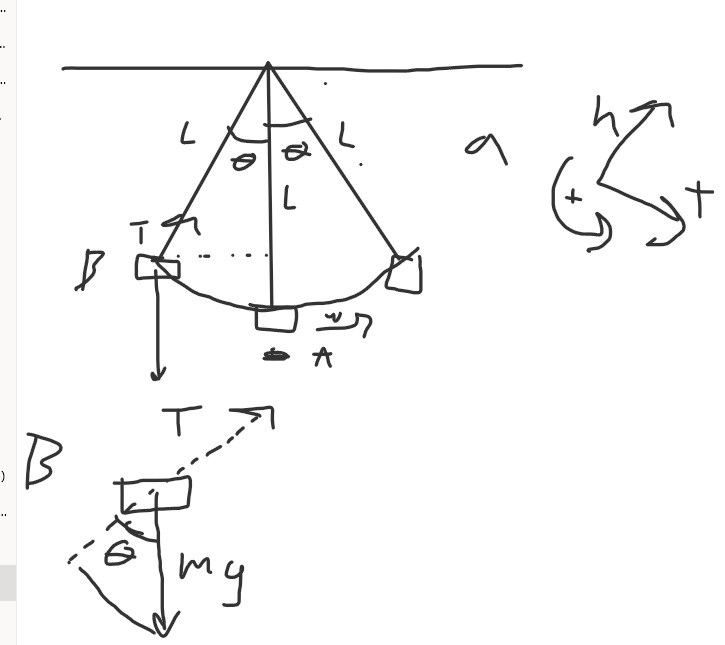
Jag tänker; $\sum_{}^{} f_{t} = m r_{c m} α = m g \sin (θ) < = > α = \frac{g \sin (θ)}{r_{c m}} ϖ = \int a d t = \frac{g t \sin (θ)}{r_{c m}} (1) m e n v i h a r ä v e n : x (t) = A \cos (w t) x' (t) - A w \sin (w t), s o m ä r s t ö r s t d å; x' (T / 2) = A w (2) 1 i 2 g e r; w_s t ö r s t = A \frac{g t \sin (θ)}{r_{c m}} (3) t i d e n s o m s ö k e s ä r t i d e n f ö r e n h a l v p e r i o d . T = 2 π \sqrt{\frac{L}{g}}, t = \frac{T}{2} = π \sqrt{\frac{L}{g}} (4) 4 i 3 ger : w_störst = A \frac{gπ \sqrt{\frac{L}{g}} \sin (θ)}{r_{cm}} = A \frac{gπ \sqrt{\frac{L}{g}} \sin (θ)}{\frac{L}{2}} = 0.20773291967504 . och svaret är 0.41546583935008 . vilket är 2 \det första svaret med tre decimaler korrekt .$

Du kan inte integrera $\displaystyle \int \alpha dt$ som du gör därför att $\theta$ förändras över tid.

Jag förstår inte vad $r_{cm}$ ska föreställa eller hur $r_{cm} = L/2$ kan stämma. Är $L$ längden på pendeln? Vad menas med bredd? Kan du visa tydligare i din figur? Tänk också på att ditt slutgiltiga uttryck inte fungerar därför att i nedersta läget är $\theta = 0$ och då skulle det bli noll.

Du bör sedan fundera på vad $x(t) = A\cos(\omega t)$ egentligen beskriver i din figur. Amplituden $A$ kan inte vara den som är given i uppgiften (90,0 ·10^-3 rad) om $x$ är ett avstånd.

Svara