Svår ekvation
Hej!
Hade behövt lite hjälp med att lösa följande andragradsekvation:
(X-5)2-(x+3)(x-3)=(x+4)2-18x
Jag har försökt några gånger men det är alltid mot slutet jag lyckas förvirra mig själv.
Min tanke var att öppna upp alla parenteser och först förenkla ekvationen så långt det gick. Jag fock på det viset bort alla x-termer. Jag får känslan av att jag gör något fel mot slutet, men kan inte sätta fingret på exakt vad.
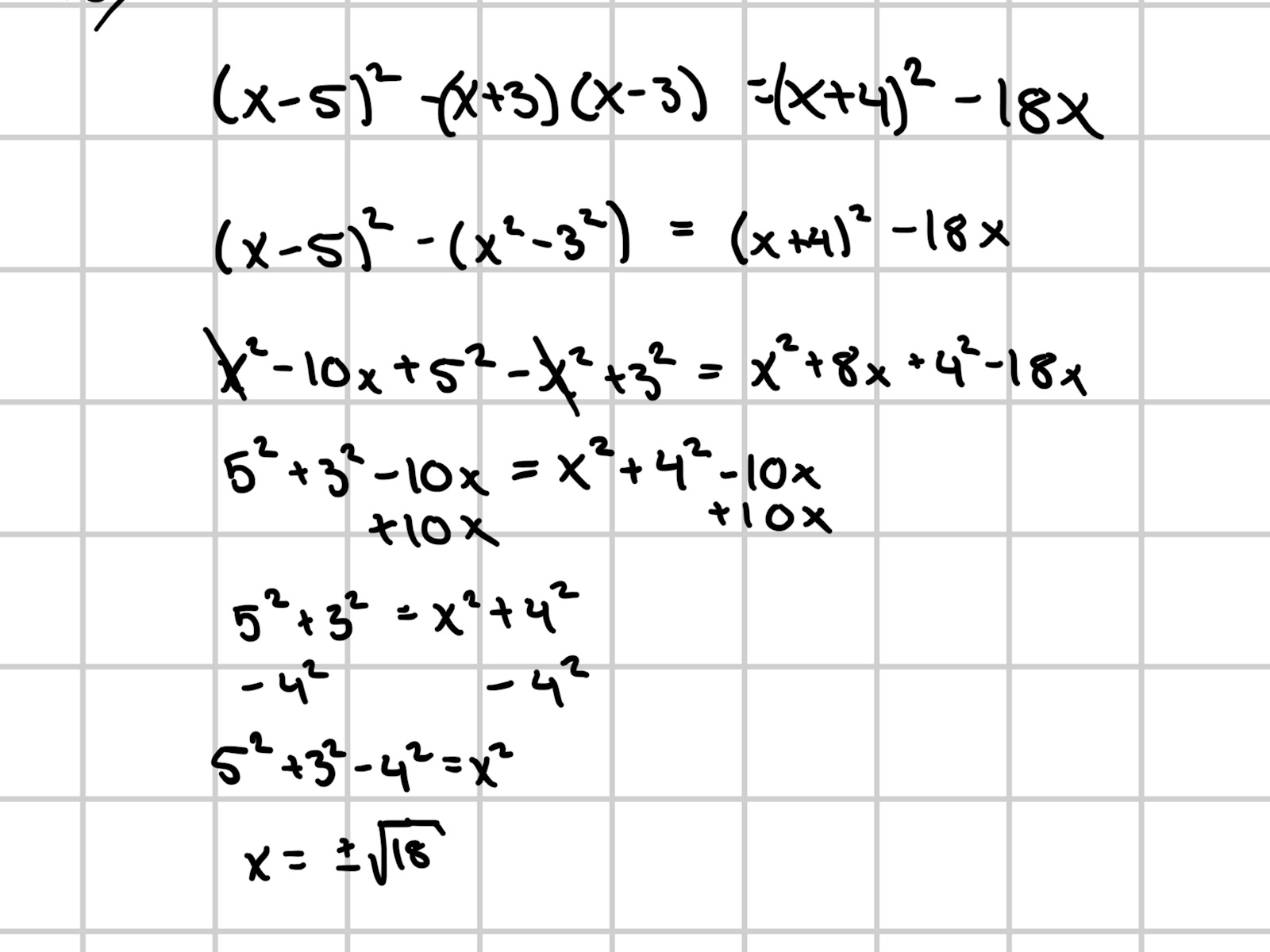
Tacksam för all hjälp :)
Jag tycker att det ser rätt ut från början till slut.
Jag instämmer. Svaret är rätt och processen ser också rätt ut. Vart tror du känslan att du gjort något fel kom ifrån?
Här är vad som står i facit och jag har inte hittat något på nätet om att det ska ha varit fel. Förstår heller inte hur det uttrycket skulle kunna skrivas om till det jag fick det till. Nu har jag också kvadrupelkollat så jag inte läst något i uppgiften fel och det har jag heller inte så vet inte vad jag missar.
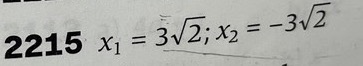
AlexMu skrev:Jag instämmer. Svaret är rätt och processen ser också rätt ut. Vart tror du känslan att du gjort något fel kom ifrån?
Den kom ifrån att jag fick ett svar som inte var vad som stod i facit😅
Svaren är densamma (testa att kvadrera ), alternativt, notera att .
Då gäller det att .
Oj, att jag inte tänkte på det viset. Det var ett litet tag sedan man räknade matte nu haha
Men då vet jag! Tack snälla för hjälpen :)
Super!
Jag tror båda svar bör vara ok om de inte skriver något som "förenkla så långt som möjligt".
Just denna gången stod det inget i den stilen. Men om det skulle göra det är facits svar rätt eftersom att det är mer förenklar än det jag kom fram till?
Jag tycker facits svar är mer förenklat, men "förenklat så långt som möjligt" är också otroligt subjektivt.
Exempelvis gäller det att . Jag tycker vänsterledet "ser snyggare" ut och jag föredrar att svara med det. Däremot är det generellt lättare att räkna med uttrycket i högerledet och jag vet inte vad man ska anse är "mest förenklat".
På liknande sätt kanske man föredrar att ha för då vet man direkt att kvadraten blir . Om man istället hade faktoriserat ut några faktorer, som facit gör, blir det inte längre direkt uppenbart vad kvadraten blir (men kanske lättare att få ett hum om vad roten har för ungefärligt värde. Exempelvis kanske man vet att och då får man direkt att , vilket kanske är svårare att direkt se från )
Jag tror att båda är ok, men jag skulle svara med att faktorisera ut, om det går.


