Svår Uppgift 5 (KTH matematikprovet)
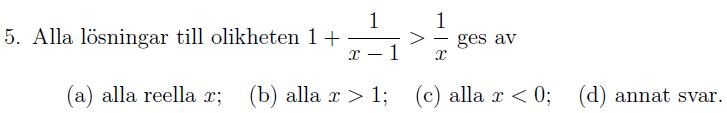
Fungerar det här?
Vad kan jag anta utifrån ekvationen längst ner?
När jag tänker efter med hjälp av pq-formeln så hajar jag att man får både ett negativt och ett positivt värde på x, därmed blir det (d) annat svart. Har jag rätt?
Jag skulle nog låtit från vänster och höger. Vad händer med olikheten då?
Du måste vara försiktig med tecknet på när du förlänger på båda sidor. Om man multiplicerar med ett negativt tal skiftar olikheten nämligen tecken.
Juste ska göra beräkningar återkommer imorgon! Tack för påpekandet.
Notera att olikheten inte bevaras om du multiplicerar med och vi har , eller om du multiplicerar med och vi har . Innan du multiplicerar olikheten med så måste du göra vissa antaganden om . För att lösa olikheten behöver vi därför betrakta olika fall, nämligen följande tre:
1. ,
2. ,
3 .
I fall 1 och 3 är olikheten ekvivalent med . Vi kan kvadratkomplettera polynomet i enligt och du ser att detta alltid är större än noll. Så olikheten stämmer för alla och alla . Så svar (b) och (c) är falska och svar (a) är uppenbarligen också falskt. Därför måste vi svara (d).
Bra förklaring Freewheeling!


