Svår Uppgift 6 (KTH matematikprovet)

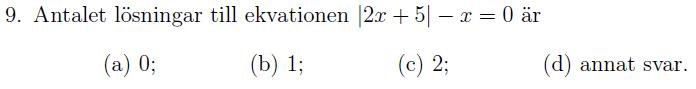
Ja strecken betecknar absolutbelopp och innebär följande .

• Om 2x+5 > 0 så är |2x+5| = 2x+5
• Om 2x+5 < 0 så är |2x+5| = -(2x+5)

Hur löser jag ut x då?

$$\begin{gathered} \left|2x+5\right|-x=0 \\ 2x+5-x=0 \\ x+5=0 \\ x=-5 \\ Då antar jag att svaret är \left(b\right) 1; \end{gathered}$$

Gör som du gjorde i Ma1, två gånger, en gång för när 2x+5>0 och en gång för 2x+5 >0 en gång för 2x+5 < 0.

EDIT: fixade en felskrivning

Smaragdalena skrev:

Gör som du gjorde i Ma1, två gånger, en gång för när 2x+5>0 och en gång för 2x+5 >0.

Jag antar att du menade:

1) $2x+5\ge 0$
samt

2) $2x+5<0$ ?

$$\begin{gathered} 2x+5>0 \Rightarrow 2x>-5 \Rightarrow x>-\frac{5}{2} \\ 2x+5<0 \Rightarrow 2x<-5 \Rightarrow x<-\frac{5}{2} \\ -\frac{5}{2}<x<-\frac{5}{2} så får det inte vara? alltså är det \left(a\right) 0; \end{gathered}$$

Har jag gjort rätt?

Du har glömt x utanför absolutbeloppet.

$$\begin{gathered} 2x+5-x>0 \Rightarrow x>-5 \\ 2x+5-x<0 \Rightarrow x<-5 \\ -5<x<-5 Vilket betyder att svaret är \left(a\right) 0; \end{gathered}$$

Antingen är $2x+5\ge 0$Då får du ekvationen $2x+5-x=0$eller så
är $2x+5<0$då får du ekvationen $-(2x+5)-x=0$

$$\begin{gathered} x>-\frac{5}{3} och x > -\frac{5}{2} \\ Såhär får det inte vara därmed drar jag slutsatsen att det är \left(a\right) 0; \end{gathered}$$

martinmaskin skrev:

$$\begin{gathered} 2x+5-x>0 \Rightarrow x>-5 \\ 2x+5-x<0 \Rightarrow x<-5 \\ -5<x<-5 Vilket betyder att svaret är \left(a\right) 0; \end{gathered}$$

Din indelning i olika fall och de respektive villkoren är inte rätt.

Gör så här:

Fall 1. 2x+5 $\geq$ 0, dvs x $\geq$ -5/2. Då gäller att |2x+5| = 2x+5 och ekvationen blir då 2x+5-x = 0. Ligger den ekvationens lösning i det tillåtna intervallet?

EDIT - Ändrade > till $\geq$ här ovan.

Fall 2. 2x+5 < 0, dvs x < -5/2. Då gäller att |2x+5| = -(2x+5) och ekvationen blir då -(2x+5)-x = 0. Ligger den ekvationens lösning i det tillåtna intervallet?

Yngve skrev:

martinmaskin skrev:

$$\begin{gathered} 2x+5-x>0 \Rightarrow x>-5 \\ 2x+5-x<0 \Rightarrow x<-5 \\ -5<x<-5 Vilket betyder att svaret är \left(a\right) 0; \end{gathered}$$

Din indelning i olika fall och de respektive villkoren är inte rätt.

Gör så här:

Fall 1. 2x+5 $\geq$ 0, dvs x > -5/2. Då gäller att |2x+5| = 2x+5 och ekvationen blir då 2x+5-x = 0. Ligger den ekvationens lösning i det tillåtna intervallet?

Fall 2. 2x+5 < 0, dvs x < -5/2. Då gäller att |2x+5| = -(2x+5) och ekvationen blir då -(2x+5)-x = 0. Ligger den ekvationens lösning i det tillåtna intervallet?

$x>\frac{-5}{3 }och x > \frac{-5}{2}$ Kan inte du istället reflektera över mitt senaste svar, där jag tar hänsyn till? −(2x+5)−x=0

Nästan rätt, men du måst koppla $2x+5\ge 0$som ger $x\ge -\frac{5}{2}$till

ekvationen $2x+5-x=0$som har lösningen $x=-5$Vilket är en motsägelse.

Den andra ekvationen ger också en motsägelse, varför det saknas lösningar.

$x>-\frac{5}{3}$och $x>-\frac{5}{2}$har däremot lösningen $x>-\frac{5}{3}$

Vad är orsaken till att det här tecknet dyker upp ≥  (förklara inte tecknet, jag vet vad det är för nåt)

martinmaskin skrev:

$x>\frac{-5}{3 }och x > \frac{-5}{2}$ Kan inte du istället reflektera över mitt senaste svar, där jag tar hänsyn till? −(2x+5)−x=0

Jag såg inte ditt svar när jag skrev mitt, men OK, jag gör det nu. Dina villkor är fortfarande inte korrekta. De ska vara $x\geq -\frac{5}{2}$ respektive $x<-\frac{5}{2}$ och de behöver inte gälla samtidigt.

Jag tror att du kanske blandar ihop olikheterna med ekvationen:

• Att 2x+5 $\geq$ 0 innebär inte att 2x+5-x $\geq$ 0.
• Att 2x+5 < 0 innebär inte att 2x+5-x < 0.

martinmaskin skrev:

Vad är orsaken till att det här tecknet dyker upp ≥  (förklara inte tecknet, jag vet vad det är för nåt)

Det har med absolutbeloppet att göra (och att absolutbeloppet av 0 är lika med 0).

Vi tittar på |a|, där a är ett vanligt uttryck.

Egentligen är det tre olika fall:

Fall 1: a > 0. Då gäller att |a| = a.

Fall 2: a < 0. Då gäller att |a| = -a

Fall 3: a = 0. Då gäller att |a| = a = -a. Detta eftersom |0| = 0 = -0.

Vi kan alltså låta fall 3 ingå antingen i fall 1 eller i fall 2. Vi kan till och med låta fall 3 ingå i båda om vi vill, men det är inte så snyggt.

Därför brukar man byta ut > mot $\geq$ när man beskriver fall 1.

Men jag glömde att göra det i mitt ursprungliga svar.

Tack Yngve det var en utomordentlig förklaring! :)