Svår uppgift gällande komplexa tal
Ge två exempel på en ekvation som kan användas för att beskriva en regelbunden hexagon(sexhörning) med avståndet 4 l.e. mellan motstående hörn?
Hur ska jag tänka här? Om z^6 = w och z = r(cosv + isinv) har jag (med hjälp av cosinussatsen) kommit fram till att r= 6. Hur kan jag gå vidare.
Tolkade frågan lite fel! r = 2 = cirkelns radie. Kan det stämma?
Anonym_15 skrev:Tolkade frågan lite fel! r = 2 = cirkelns radie. Kan det stämma?
Ja, det ska det vara.
Men hur går jag vidare?
Jag tänkte så här: vi vet enbart absolutbeloppet av z och att perioden för argumentet är 60 grader. Jag ansätte därför vinkeln till 0 grader i ett fall och 30 grader i ett annat fall. Går det att göra så? Jag fick följande svar:
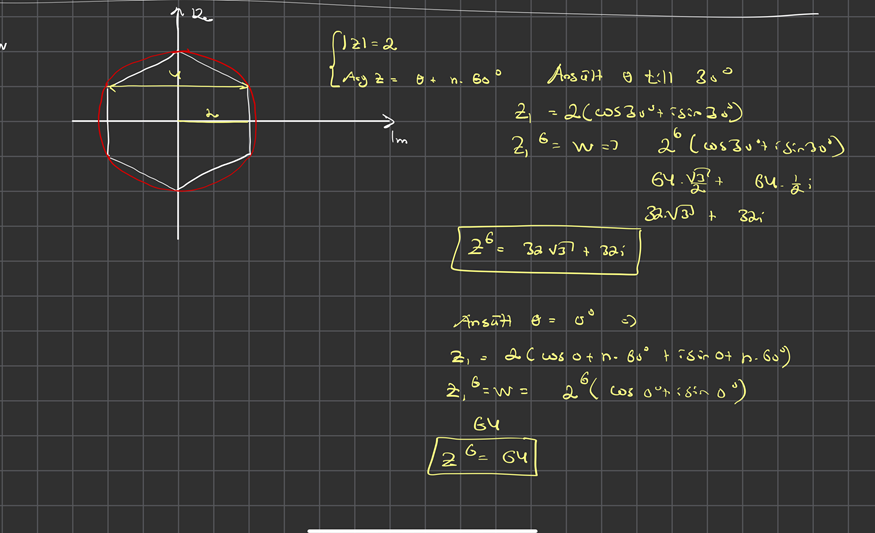
Njae... När du upphöjer med 6 ändras absolutbeloppet (det har du rätt) men även argumentet, det är inte fixt vid 30°
Vad menas med att argumentet inte fixas? Hur ska jag då veta att det just är vid 0 grader? Vad var den andra lösningen?
Anonym_15 skrev:Vad menas med att argumentet inte fixas? Hur ska jag då veta att det just är vid 0 grader? Vad var den andra lösningen?
Här ser vi ett typexempel på hur fel det kan gå med polär form då den inte är aritmetiskt naturlig.
om z = r (cos t + i sin t) är z^n = r^n (cos nt + i sin nt)
Det blir fel här
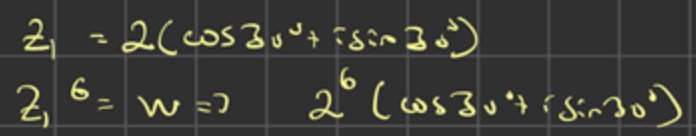
Så hur vet jag vilka vinklar det gäller?
Är fortfarande lite osäker på hur ekvationen kan lösas.
z^6 = 2^6( cos(30*6) + i sin(30*6) ) =64( (-1) + i (0) ) =-64
Och hur visste du att enbart två vinklar kunde användas? Hur kom du fram till dessa två som gav svaren 64 och -64?
Anonym_15 skrev:Och hur visste du att enbart två vinklar kunde användas? Hur kom du fram till dessa två som gav svaren 64 och -64?
Det finns oändligt många ekvationer, men uppgiften frågade efter 2 exempel. Alla hexagoner, men en vinkelförskjutning funkar. Vi bara väljer 0 och 30° för det ger snygga ekvationer.


