1
svar
81
visningar
Anonym_15 behöver inte mer hjälp
Svår uppgift gällande matematisk induktion...
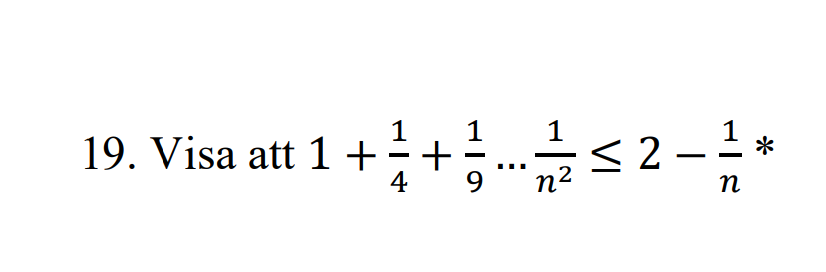
Jag vill bevisa följande.
Enligt facit:
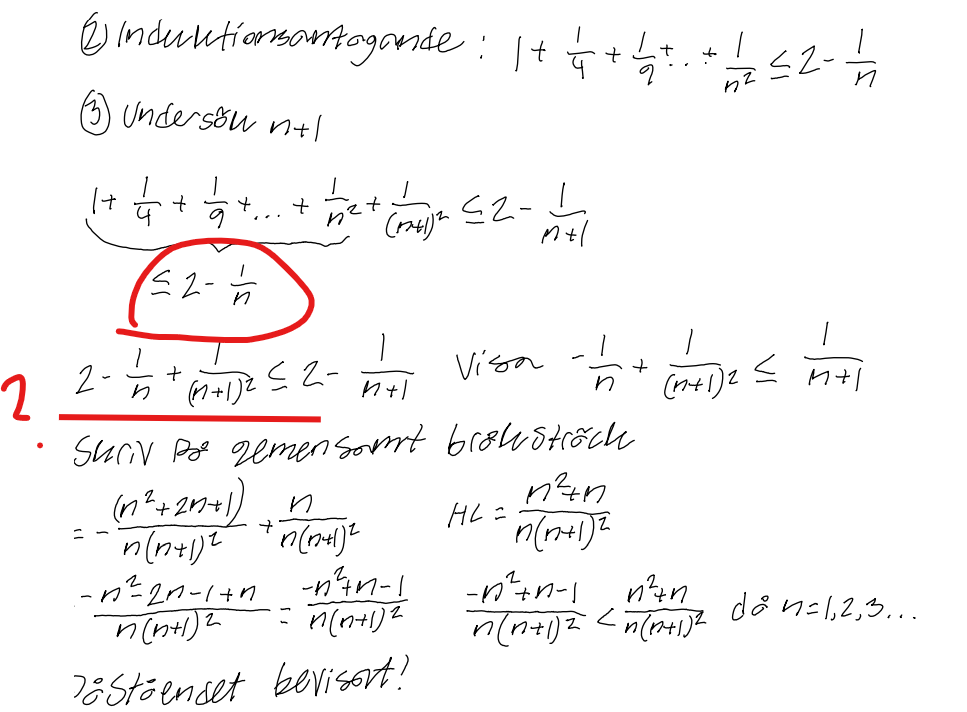
Jag förstår ej hur induktionsantagandet kan användas. Hur vet man med säkerhet att 2 - 1/n + 1/(n+1)^2 med säkerhet är mindre än 2 - 1/n+1?
Ett sätt att visa att
är flytta runt lite, vilket ger det ekvivalenta påståendet
Vi sätter allt på samma bråkstreck i VL, vilket ger
Multiplicera nu båda led med och utveckla parentesen i nämnaren, vilket ger att påståendet från början är ekvivalent med
Vilket är ett rätt uppenbart sant påstående. Täljaren är liite större än nämnaren.

