Svår uppgift gällande rekursionsformler
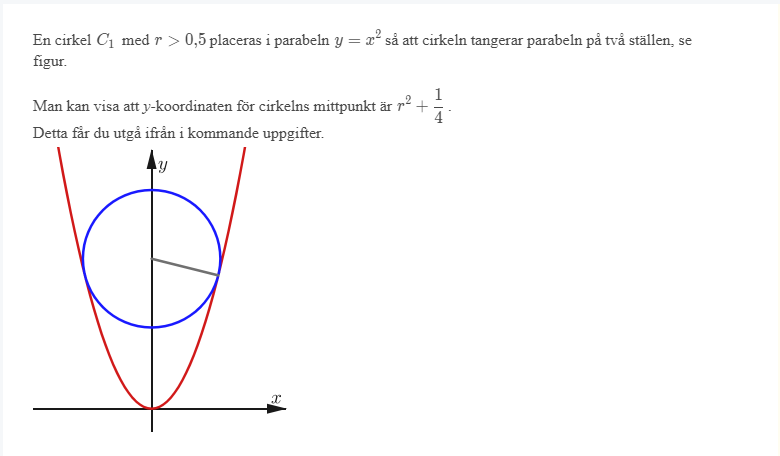
a) har jag löst och fick fram rätt svar som facit:
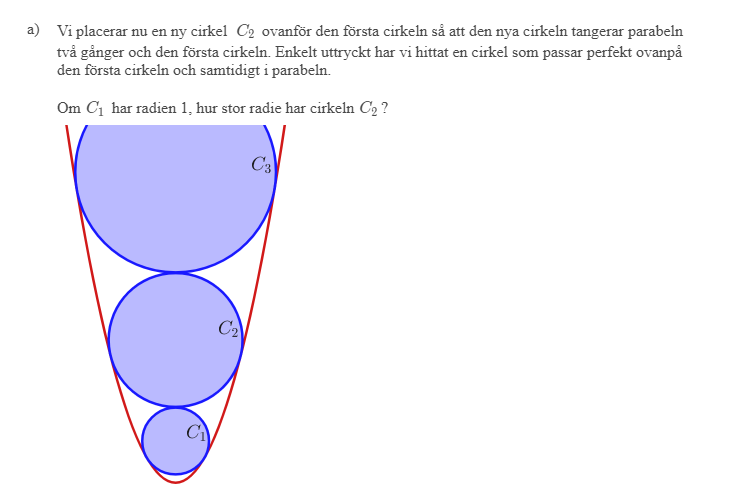

Det är b och c som jag inte förstår:

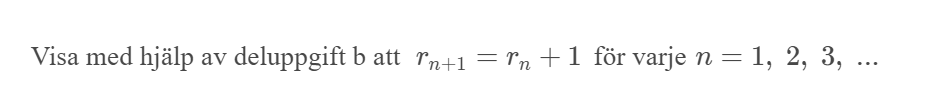
Jag tror att om jag kan få reda på hur b ska lösas kan jag ta mig vidare därifrån.
När du tittar på a-uppgiftens facit:
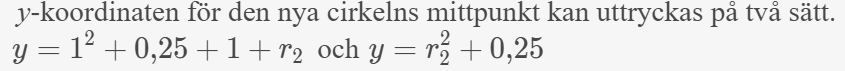
förstår du hur de kom på dessa två uttryck för y?
Likheten i b-uppgiften kan nämligen bevisas enligt exakt samma princip som utnyttjades i a-uppgiften.
Visa spoiler
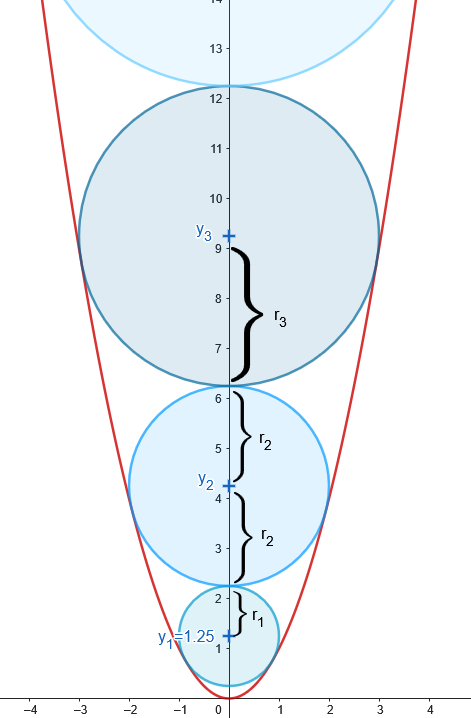
Kolla i figuren ovan. Antag att:
- y-koordinaten för mittpunkten av :te cirkeln betecknas med .
- radien av :te cirkeln betecknas med
(a)-uppgiften:
kan uttryckas på två sätt:
- Det var givet att .
- Man kan gå från uppåt med steg, så . Det var givet att och därmed . Dessa insatta i ger att
Det är olika uttryck för samma storhet (), så de är lika:
Radien är positiv, så .
(b)-uppgiften
Samma resonemang används. kan uttryckas på två sätt:
- Det var givet att .
- Man kan gå från uppåt med steg, så . Det var givet att . När detta sätts in i , så fås att .
Det är olika uttryck för samma storhet (), så de är lika:
När man flyttar över till VL och subtraherar från båda leden, så får man att , vilket skulle visas.
Tack! Nu förstår jag både a och b. Jag har länge försökt med c men kommer ingen vart.
Utgå från sambandet , som kan skrivas om som .
Detta är en andragradsekvation i variabeln , så man kan lösa ut m.h.a. pq-formeln, där och
Visa spoiler
.
Enligt kvadreringsformeln baklänges är , så man kan faktiskt lätt dra kvadratroten:
, vilket ger alltså att
- (falsk lösning)
eller - (sann lösning)
Precis så löste facit uppgiften. Men får man ansätta rn+1 till en variabel? Varför? I vilka fall kan jag göra det? Facit säger att det gäller eftersom rn+1 beror av rn på samma sätt som y beror av x.
Går det också att lösa med hjälp av induktion?
Anonym_15 skrev:Går det också att lösa med hjälp av induktion?
Vilket jag försökte med.
Anonym_15 skrev:Precis så löste facit uppgiften. Men får man ansätta rn+1 till en variabel? Varför? I vilka fall kan jag göra det? Facit säger att det gäller eftersom rn+1 beror av rn på samma sätt som y beror av x.
Det finns två symboler i sambandet , nämligen och . Namnet på de här symbolerna är oväsentligt så länge man är konsekvent med beteckningen. Sambandet kan lika gärna skrivas om som ifall man döpt om och .
Sambandet kan betraktas som en ekvation och då kan man lösa ut ur denna ekvation (vilket jag gjorde i #4). Enligt frågeställningen är det exakt som man vill lösa ut, så det känns naturligt att göra just det. Det går dock lika bra att lösa ut istället:
är en andragradsekvation i variabeln . pq-formeln ger då att
Man kommer fram till . På så sätt har man visat att , vilket är ekvivalent med det man ville visa. Notera dock att man löst ut och man behöver ta ett till steg (flytta över ettan) för att lösa ut , vilket man egentligen var ute efter.
Anonym_15 skrev:Går det också att lösa med hjälp av induktion?
Njae... ser inte hur induktion skulle funka. Induktionssteget i detta fall skulle innebära att man ville visa följande:
- Om man redan vet att gäller för något specifikt värde på , så kan man dra slutsatsen att också gäller för det värdet på .
Ett sådant påstående är inte sant om man inte dessutom förutsätter att gäller för . (Denna förutsättning är visserligen uppfylld, men då behövs inte induktionsantagandet.)

