Talföljd.. Induktion..
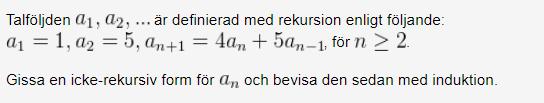
Är helt lost på denna typen av uppgifter.. Kan någon peka lite lätt åt ett håll för mig att börja på? :) Hade uppskattats!
Håller på att läsa om induktion i boken just nu, men har precis börjat med det.
Börja med att ta fram några siffror i talföljden (genom den rekursiva formeln):
Vilken icke-rekursiv formel skulle det kunna handla om? :)
Smutstvätt skrev:Börja med att ta fram några siffror i talföljden (genom den rekursiva formeln):
Vilken icke-rekursiv formel skulle det kunna handla om? :)
?
Helt rätt! Nu behöver vi genomföra tre steg:
1. Basfall
2. Induktionsantagande
3. Induktionssteg (användande av antagandet)
Vi kan börja med basfallet. Vi kan använda basfallet . Stämmer formeln för detta fall? :)
Smutstvätt skrev:Helt rätt! Nu behöver vi genomföra tre steg:
1. Basfall
2. Induktionsantagande
3. Induktionssteg (användande av antagandet)
Vi kan börja med basfallet. Vi kan använda basfallet . Stämmer formeln för detta fall? :)
Nej.. Så formen är ? Då stämmer det?
Det beror på vilket n vi börjar på, men ja jo, är nog en bättre formel. Vi kör på den istället. :) Eftersom vi har en rekursiv formel som inkluderar två föregående tal, behöver vi två basfall och två antaganden.
Okej, så det stämmer för . Bra! Stämmer formeln för ?
Nu gör vi ett induktionsantagande, och antar att formeln stämmer för , dvs. att . Vi lär även behöva ett liknande antagande för .
Vi vill nu på något vis använda detta antagande för att visa att . :)
Smutstvätt skrev:Det beror på vilket n vi börjar på, men ja jo, är nog en bättre formel. Vi kör på den istället. :) Eftersom vi har en rekursiv formel som inkluderar två föregående tal, behöver vi två basfall och två antaganden.
Okej, så det stämmer för . Bra! Stämmer formeln för ?
Nu gör vi ett induktionsantagande, och antar att formeln stämmer för , dvs. att . Vi lär även behöva ett liknande antagande för .
Vi vill nu på något vis använda detta antagande för att visa att . :)
Ja det stämmer in för också, och vidare till
Så då har vi två basfall. Men är helt borta efter det.. Sitter och läser på matteboken.se om induktion ihop om att bli klokare.
Men när jag ska bygga mitt bevis så har jag "vänsterledet" avklarat, det är ju min befintliga formel som jag vet stämmer.
Vi vill bevisa att , givet våra ursprungsvärden.
Vi har gjort antagandena att , samt . Vi vill nu bevisa att .
Den rekursiva formeln säger att . Stämmer det att ? :)
Smutstvätt skrev:Vi vill bevisa att , givet våra ursprungsvärden.
Vi har gjort antagandena att , samt . Vi vill nu bevisa att .
Den rekursiva formeln säger att . Stämmer det att ? :)
Vill säga ja, att det stämmer. Men kan inte förklara varför jag vill säga ja.. haha.
Prova! Sätt in antagandena istället för och och förenkla. :)
Smutstvätt skrev:Prova! Sätt in antagandena istället för och och förenkla. :)
Jag får
Så lång kom jag, vet inte hur jag ska hantera ?
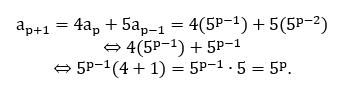
Löste det :)
Du är på rätt spår! Våra antaganden är att och . Vi har den rekursiva formeln , och vi vill bevisa att formeln . Vi sätter in våra induktionsantaganden i den rekursiva formeln, och får då:
Stämmer formeln? :)


