Talföljd problem
Skulle behöva lite hjälp att förstå innebörden av de olika talen. Hur man får ett svar med hjälp av geometrisk summa.
Elin och Karl vill låna 1 200 000 kr till ett hus. Räntesatsen är 4,75 % och de ska betala tillbaka lånet på 25 år med lika stora inbetalningar (ränta+amortering) varje månad. De tänker avsätta 10 000 kr/månad till bostadslånet. Räcker det?
Vilka tal är det du behöver hjälp med?
Är 4,75% en årsräntesats?
Står det något mer i uppgiftstexten (eller i kapitlet där uppgiften står)?
Nej tyvärr inte, denna uppgiften hittade jag på kunskapsmatrisen. Det enda som jag fick som facit var: Godtagbar ansats, t ex omvandlar till månadsränta och påbörjar beräkning med geometrisk summa av kontinuerligt sparande med 10000 kr/månad eller påbörjar beräkning av storleken på annuiteterna.
Finns även en b) som lyder
Efter några år stiger räntan med 0,5 procentenheter. Har de då råd att betala av lånet? Något jag inte alls förstår
Den här artikeln kan hjälpa dig att förstå
Har kollat på många förklaringar om fenomenet men inte hur man löser med hjälp av geometrisk summa,
Ekvationen för annuiteten i beskrivningen är en geometrisk summa.
Hos oss har vi lärt oss följande formel: sn=a1*(kn-1)/(k-1)? Och genom att använda Wikipedias formeln får jag inte rätta svar.
Den gäller här också.
Frågan är hur termerna ser ut i den summa som ska beräknas.
Då måste man känna till en del ekonomiska begrepp och samband.
Är du bekant med begreppen nuvärde och nuvärdesumma?
Här finns en räknare https://www.kreditkoll.nu/rakna-pa-lan#tabs
Pröva att sätta in dina värden i den och se vad du får.
Det kommer nog inte att stämma med facit men inte långt ifrån.
Är du bekant med begreppet effektiv räntesats?
Jag studerar natur och detta är inget vi har gått igenom förutom geometrisk summa
Då blir det besvärligt att lösa en uppgift som denna.
Det gäller att bestämma x (månadsbetalningen) så att
summa nuvärde av de framtida betalningarna blir lika med lånebeloppet.
(fortsättning)
Matematiskt betyder det att du ska lösa ekvationen
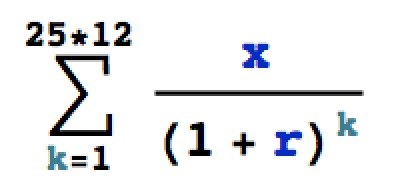= 1 200 000
där r är månadsräntesatsen (som decimalbråk), som i detta slags exempel brukar sättas till en tolftedel av årsräntesatsen. Här: 4,75%/12 = 0,0475/12 .
