talteori
Förstår inte alls vad de gör här, jag trodde man skulle ta MGM?
När vet jag när jag ska ta MGM eller SGF?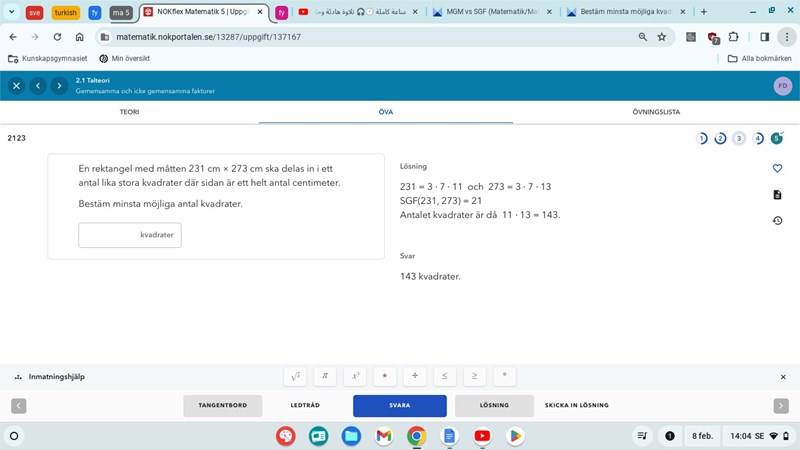
Om du ska använda SGF eller MGM beror på vad uppgiften gäller och vad det ör du är ute efter.
I det hör fallet vill de veta det minsta möjluga antalrt kvadrater, vilket innebär att vi vill att kvadraterna ska vara så stora som möjligt.
Pröva med att göra kvadrater med hjälp av MGM istället. Hur många kvadrater får du då?
får 4719, men grejen är de tar inte ens SGF utan de multiplicerar 11 med 13?
231 = 21 * 11
273 = 21 * 13
Alltså är det 11*13 kvadrater i rektangeln, 13 på bredden och 11 på höjden.
men vad är det som man räknar ut? det varken MGN eller SGF?
Jo, det gör man.
- Det ena talet består av faktorerna 3, 7 och 11.
- Det andra talet består av faktorerna 3, 7 och 13.
Den största gemensamma faktorn är därför 3*7 = 21.
De största möjliga kvadraterna kommer alltså att ha sidlängden 21
Primtalsfaktorisera både 231 och 273 och undersök om de har någon gemensam faktor. Om de inte har någon gemensam faktor kan man lägga rektangeln med småkvadrater med sidan 1 cm, men det blir många!
Ja vet att 21 är största gemensamma faktorn, men vad ger det mig för information? hur vet jag att det är sidolängden?
De enda möjliga storlekarna på kvadrater så att det ändå går jämnt ut är
- 1x1
- 3x3
- 7x7
- (3*7)x(3*7), dvs 21x21
SGF ger oss alltså den största möjliga storleken på kvadrater så att det ändå går jämnt ut.
okej tack!



