Tan(4x) = .... Bevis!
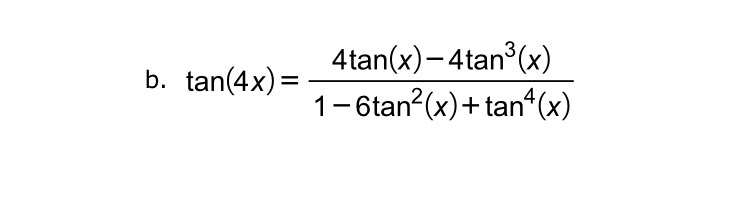
Hur arbetar jag med HL här?
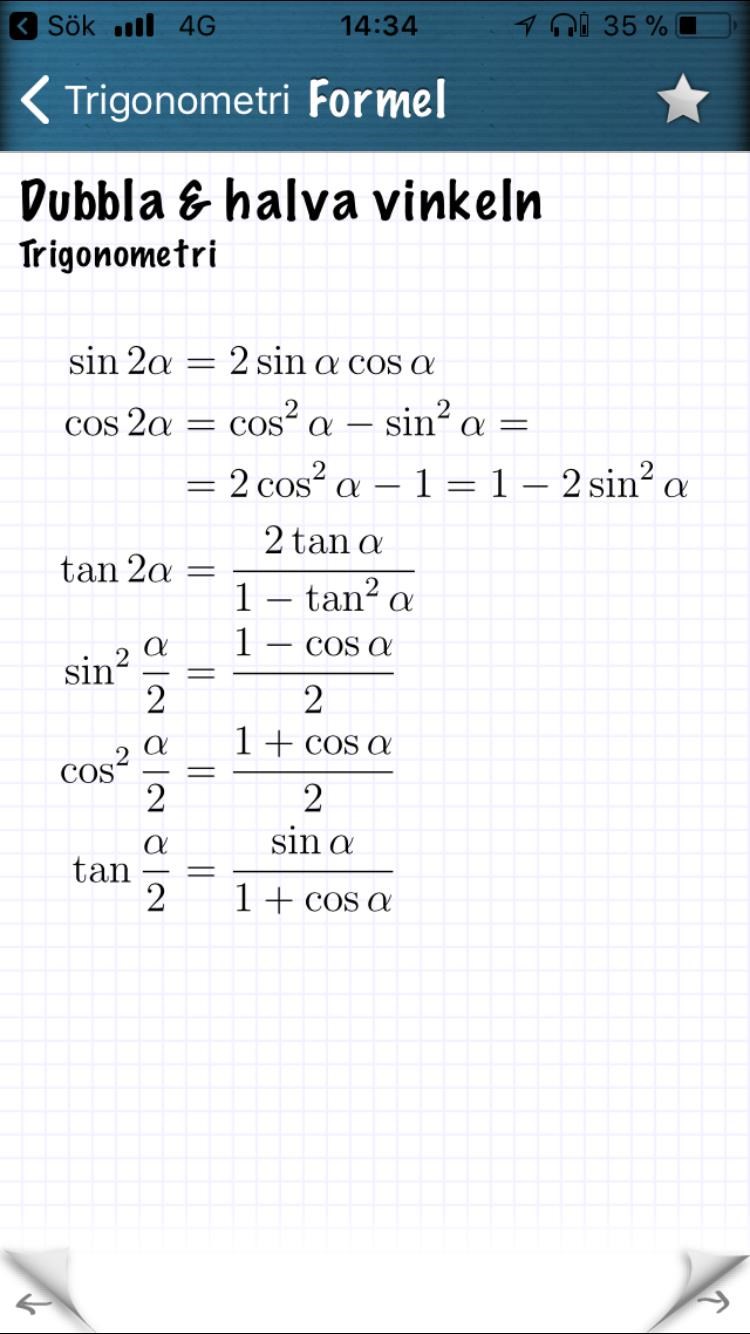 Jag skulle säga att det är bättre att börja med VL utifrån formeln för dubbla vinkeln (se ovan).
Jag skulle säga att det är bättre att börja med VL utifrån formeln för dubbla vinkeln (se ovan).
Vill du utveckla lite mer? VL skulle alltså i första steget ge?
Sätt . Vad blir då
?
Agh, dessa identiteter. Blir inte klok på dom.
Sitter på telefonen så kan inte infoga en ekvation.
Men jag tänkte: tan(4x) —> tan2(2x) = 2tan2x / 1-tan^2x
Men vet inte hur jag ska gå vidare. Jag lärde mig att man ska försöka börja med det led som ser krångligast ut, samt att tan oftast ska omvandlas till sin/cos om man inte vet hur man ska gå vidare. Därför är detta lite förvirrande 😅
Korrekt! Vad blir då uttryckt i termer av ?
De regler du hänvisar till gäller oftast, men just detta fall är ett undantag.
tomast80 skrev:Korrekt! Vad blir då uttryckt i termer av ?
Multipl. nämnaren med 2?! Sorry riktigt kass på detta moment. Stort tack för hjälpen!
Titta på listan som tomast80 skrev in tidigare. Där finns det en formel som visar vad är i termer av . Om du sätter in 2x på alla ställen där det står x (och 4x där det står 2x) får du en formel som visar vad är i termer av . Sedan kan du använda samma formel en gång till på den nya formeln och så småningom få fram är i termer av .
Är det samma som att sätta in 4x resp 8 x där det står x resp 2x? Eller läraren vill se samtliga steg.
Du skall göra alla steg.
Hej!
.
Albiki skrev:Hej!
.
Sätt in uttrycket för tan2x på alla ställen där det står tan2x i den övre ekvationen. Förenkla. Då bör du komma fram till HL i frågan.
 Vad gör jag för fel här? Ursäkta slarvigt skrivet, ska renskriva sen.
Vad gör jag för fel här? Ursäkta slarvigt skrivet, ska renskriva sen.
Albiki skrev:Hej!
.
Varför följer du inte de råd du får? Följ det som Albiki skrev, och gör uppgiften i två steg, så kommer det nog att gå bättre.
Varför jag inte följer råd? Jag gör så gott jag kan, även om du inte verkar tro det. Har svårt att greppa detta moment.
F.ö följer jag ditt råd, se nedan.
Smaragdalena skrev:Albiki skrev:Hej!
.
Sätt in uttrycket för tan2x på alla ställen där det står tan2x i den övre ekvationen. Förenkla. Då bör du komma fram till HL i frågan.
Du har rätt, jag såg inte att du hade försökt längre ner på ditt kladdiga papper.
Om du använder dig av formelskrivaren finns det en större chans att det går att tyda det du skriver.
Skriv tan(x)+tan(x) som 2tan(x) och tan(x)tan(x) som på alla ställen, så reder det nog upp sig.



