Tangenter som inte skär varandra
Uppgift: "Kan en kurva ha tangenter som inte skär varandra? Motivera"
Facit: "Ja, t.ex. tangenterna i en maximipunkt och en minimipunkt på en kurva. Båda är horisontella och skär därför inte varandra".
Någon mer som tycker att svaret inte besvarar uppgiften korrekt?
"Kan en kurva ha tangenter som inte skär varandra? Motivera"
Vad tycker du saknas i deras svar?
Jag tycker inte att facit besvarar uppgiften, vad tycker du?
Jag tycker frågan är besvarad =) Menar du att ett exempel inte är en motivering, eller var ligger problemet? Förstår inte riktigt vad din invändning är.
Jag ska förklara men svara först på följande fråga tack.
Hur många kurvor har denna graf skulle du säga? 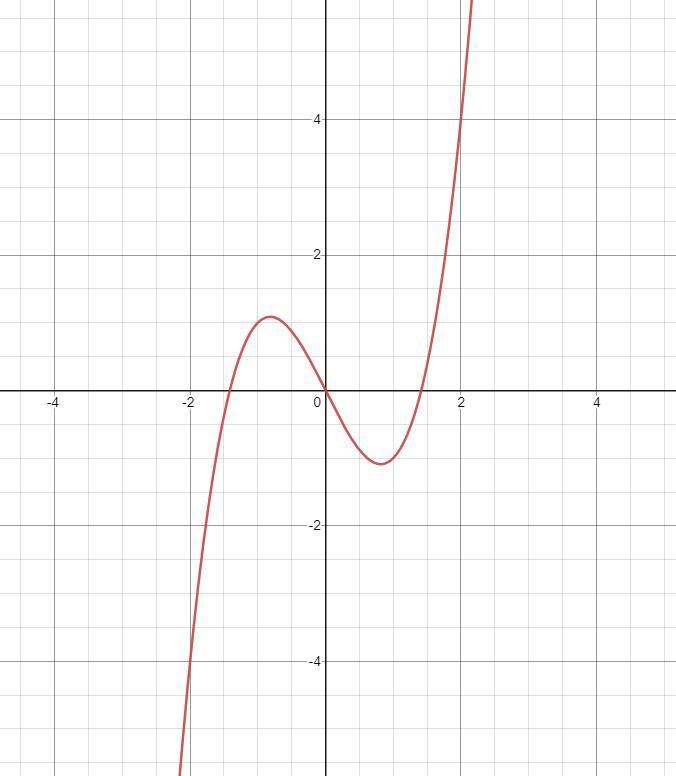
En? Det här blir allt mer kryptiskt. Kurvan är ju själva funktionen, och jag ser en sån utritad. Den är röd. =)
Så om jag säger att denna figur har två stora kurvor, är det ett felaktigt påstående enligt dig?
Menar du själva buktningarna på funktionen? Ja, jag skulle tycka det är felaktigt att kalla dem kurvor. En kurva är i såna här sammanhang inte "en böj", utan den del i bilden som är själva funktionen. Även en rät linje är en kurva, i den betydelsen.
De fem synonymer som nämns i den övre del av denna hemsida är felaktig påstår du därmed?
https://www.ordguru.se/synonymer/kurva
Varför tittar du på synonymer? Titta på ordets beskrivning istället. Den matematiska innebörden har inget med svängar att göra, och det är väl fullt möjligt att det saknas synonymer för just den betydelsen.

Enligt den definition betyder kurva inte samma sak inom matematik som det gör i vardagligt språkbruk. Jag tolkade uppgiften som att man beskriver "en kurva". Inte en matematisk kurva utan en kurva i det vardagliga språket. Och om man har en graf som bara har "en kurva" då finns det ingen tangent som inte skärs av minst en annan tangent.
Denna definition av kurva ska finnas i boken eller tidigare böcker av denna serie tycker jag.
Om man vet att ordet kurva har den definitionen inom matematiken blir det lätt att lösa uppgiften.
Skaft skrev:En? Det här blir allt mer kryptiskt. Kurvan är ju själva funktionen, och jag ser en sån utritad. Den är röd. =)
Jag tror du vet vad jag menar men du vill bara ställa till det. Om du hade fått en väginstruktion som säger: Sväng till höger efter du har passerat två kurvor.
Då hade du förstått när du ska svänga höger.
Ämnet är ju matematik, inte bilkörning. Vad anser du om ordet "sinuskurva"?
Lite konstig känsla när man hoppar in i en tråd för att reda ut missförstånd och blir anklagad för att vilja "ställa till det". Det var inte alls tydligt för mig vad du menade, och du väntade många inlägg med att förklara det.
Men ja, "kurva" är ett av flera ord som har olika betydelser i mattevärlden och utanför. "funktion" är ju också ett sånt. Det skapar förvirring och är inte så konstigt. Sen förstår jag inte riktigt vart du vill komma med väginstruktionen, men som sagt, ordet tolkas olika i olika sammanhang.
Laguna skrev:Ämnet är ju matematik, inte bilkörning. Vad anser du om ordet "sinuskurva"?
En bonde säljer 5 apelsiner för 5kr styck, hur mycket pengar får bonden för alla apelsiner? Korrekt svar: 50kr, inom matematiken betyder 1 apelsin egentligen två apelsiner. Detta är självklart för det handlar om matematik och där har olika ords ursprungliga betydelse skiftats lite ibland. Detta är "logiskt". Det är vad du försöker argumentera för med din kommentar: "Det är ju matematik".
Det finns ingen självklarhet att man inom matematiken behöver tolka alla ord annorlunda, definitionerna är något som man bör känna till innan. Det är varken mer eller mindre självklart att begrepp ska ha en helt annan betydelse bara för det handlar om ett annat ämne.
Ordet utvecklas av människor och det ena är inte mer självklart än det andra. Din kommentar är irrelevant och den är inte så självklar som du verkar tro.
Sinuskurva är ett annorlunda begrepp, det är mer begripligt tycker jag eftersom ordet "kurva" sitter ihop med "sinus". Och ja, om jag skulle besvara vad en sinuskurva är då hade jag sammanfattat alla "kurvor" som en kurva.
Skaft skrev:Lite konstig känsla när man hoppar in i en tråd för att reda ut missförstånd och blir anklagad för att vilja "ställa till det". Det var inte alls tydligt för mig vad du menade, och du väntade många inlägg med att förklara det.
Men ja, "kurva" är ett av flera ord som har olika betydelser i mattevärlden och utanför. "funktion" är ju också ett sånt. Det skapar förvirring och är inte så konstigt. Sen förstår jag inte riktigt vart du vill komma med väginstruktionen, men som sagt, ordet tolkas olika i olika sammanhang.
Jag frågade om din definition av kurva med hjälp av en bild på en figur. Du valde att bara yttra dig med den matematiska definition, trots att du kände till den andra definitionen av kurva också. Du kanske undanhöll den definitionen med flit eller så var du bara otydlig. Om du var otydlig då tar jag tillbaka att du ställde till det.
Att du upplever en konstig känsla förstår jag inte, beskriv den konstiga känslan.
Ja, jag håller med om att det skapar förvirring.
Matte är kul, småbråk på internet är det inte. Är vi då överens om att det inte är nåt trasigt med uppgiften eller facits svar?
Skaft skrev:Matte är kul, småbråk på internet är det inte. Är vi då överens om att det inte är nåt trasigt med uppgiften eller facits svar?
Jag definierar inte texten ovan som ett bråk, snarare en diskussion. Ibland behöver diskussioner lite spirit.
Nej vi är inte överens om det, uppgiften saknar tydlighet med tanke på att denna definition av kurva in nämnts i boken eller seriens tidigare böcker. Tycker du att en gymnasieelev ska betygsättas på en sådan fråga utan att någonstans ha fått någon sådan definition av kurva tidigare?
Vi är däremot överens om att uppgiften inte är trasig om man även har blivit upplyst om en kurvas definition inom matematiken.
Matte 3 är knappast första gången en elev möter ordet "kurva" i betydelsen "ritad funktion". Ibland förtydligar man genom att säga "funktionskurva", men ordet betyder samma sak även utan det prefixet. Jag skulle påstå att det är ganska väletablerat. Du tycker säkert annorlunda.
Med det sagt så känner jag mig klar här. Är det diskussion du vill ha så föreslår jag att du mjukar upp tonen en aning. Du kanske kallar det "spirit", men jag tycker bara det låter otrevligt med anklagelser om mina intentioner, att jag "undanhåller" saker etc. Håll dig till saken istället, och kanske förtydliga din egen position tidigare så blir det lättare att bemöta den.
I matteboken.se används ordet kurva en massa gånger, men man gör aldrig tydligt i ord att en kurva kan ha flera böjar. Däremot finns det ett sådant exempel på ett ställe.
Man får hoppas att läraren ger tillräcklig information om det här.
För övrigt håller jag med Skaft.
Skaft skrev:Matte 3 är knappast första gången en elev möter ordet "kurva" i betydelsen "ritad funktion". Ibland förtydligar man genom att säga "funktionskurva", men ordet betyder samma sak även utan det prefixet. Jag skulle påstå att det är ganska väletablerat. Du tycker säkert annorlunda.
Med det sagt så känner jag mig klar här. Är det diskussion du vill ha så föreslår jag att du mjukar upp tonen en aning. Du kanske kallar det "spirit", men jag tycker bara det låter otrevligt med anklagelser om mina intentioner, att jag "undanhåller" saker etc. Håll dig till saken istället, och kanske förtydliga din egen position tidigare så blir det lättare att bemöta den.
Hänvisa till en populär mattebok upp till matte 3. bok där man definierar en kurva på sådant sätt. Bevisa din teori.
Jag beskrev tydligt vad jag menade med att du ”undanhåller” och jag skrev även att jag tog tillbaks det om du inte menade så. Jag har hållit mig till saken i denna tråd hela tiden. Du anklagar mig just nu.
I matte 2 lär man sig om kurvor så det borde redan då vara etablerat vad en kurva är. Jag tycker inte uppgiften är otydlig. Det är viktigt att kolla på sammanhanget.
Man kunde varit tydligare med att använda ordet funktion eller något liknande men i matte 3 tycker jag man ska veta vad som avses. Jag kan ha förståelse för din tolkning men helt ärligt hade jag aldrig tänkt på det om du inte nämnt det.
Se upp med tonen i tråden också, det börjar bli lite dålig stämning. /Moderator
Dracaena skrev:I matte 2 lär man sig om kurvor så det borde redan då vara etablerat vad en kurva är. Jag tycker inte uppgiften är otydlig. Det är viktigt att kolla på sammanhanget.
Man kunde varit tydligare med att använda ordet funktion eller något liknande men i matte 3 tycker jag man ska veta vad som avses. Jag kan ha förståelse för din tolkning men helt ärligt hade jag aldrig tänkt på det om du inte nämnt det.
Se upp med tonen i tråden också, det börjar bli lite dålig stämning. /Moderator
Visa vart denna matematiska definition av kurvor förekommer i ma2 tack. Gärna en populär bok som matematik 5000.
Korra skrev:Dracaena skrev:I matte 2 lär man sig om kurvor så det borde redan då vara etablerat vad en kurva är. Jag tycker inte uppgiften är otydlig. Det är viktigt att kolla på sammanhanget.
Man kunde varit tydligare med att använda ordet funktion eller något liknande men i matte 3 tycker jag man ska veta vad som avses. Jag kan ha förståelse för din tolkning men helt ärligt hade jag aldrig tänkt på det om du inte nämnt det.
Se upp med tonen i tråden också, det börjar bli lite dålig stämning. /Moderator
Visa vart denna matematiska definition av kurvor förekommer i ma2 tack. Gärna en populär bok som matematik 5000.
Jag har ingen matte 2 bok tyvärr men det står tydligt här.
https://www.matteboken.se/lektioner/matte-3/derivata/tangentens-lutning
Hur tolkar du kurva här? Det avses tydligt att man menar grafen, dvs funktionen oxh inte extrempunkter.
Dracaena skrev:Korra skrev:Dracaena skrev:I matte 2 lär man sig om kurvor så det borde redan då vara etablerat vad en kurva är. Jag tycker inte uppgiften är otydlig. Det är viktigt att kolla på sammanhanget.
Man kunde varit tydligare med att använda ordet funktion eller något liknande men i matte 3 tycker jag man ska veta vad som avses. Jag kan ha förståelse för din tolkning men helt ärligt hade jag aldrig tänkt på det om du inte nämnt det.
Se upp med tonen i tråden också, det börjar bli lite dålig stämning. /Moderator
Visa vart denna matematiska definition av kurvor förekommer i ma2 tack. Gärna en populär bok som matematik 5000.
Jag har ingen matte 2 bok tyvärr men det står tydligt här.
https://www.matteboken.se/lektioner/matte-3/derivata/tangentens-lutning
Hur tolkar du kurva här? Det avses tydligt att man menar grafen, dvs funktionen oxh inte extrempunkter.
Denna fråga uppstår i en matte 3 bok (matematik 5000 +version) innan kapitlet om derivator.
Man definierar inte ordet för kurva i det du länkade man bara använder den matematiska definitionen när man uttrycker sig. Fast det är ingen direkt förklaring. (Om inte jag missade någon del i texten)
Jag vet nu hädanefter att det finns en matematisk definition på ordet kurva och att det är så man bör uttrycka sig när man pratar om matematik på svenska. Jag visste inte det innan. Och jag har heller inte blivit informerad om det.
I origo 2c är man tydlig:

Inom matematisk analys så brukar man se en kurva som bilden av en kontinuerlig funktion från ett intervall till ett topologiskt rum.
Vissa ord har en väldigt specifik betydelse inom sina fackområden, men en mycket mer lös, tvetydig eller oklar tolkning i det vardagliga språket. Kurva är ett sådant, några andra är:
- Energi
- Kraft
- Palindrom
- Symbios
Bara inom medicin lär det finnas några dussin ord som används på ett sätt inom medicinska yrken, och på ett annat sätt i vardagen, särskilt om vi räknar in ord som används i en vidare eller snävare betydelse än fackligt korrekt. Det gäller att hålla isär olika användningar av orden, och då hänger mycket på sammanhanget. I detta fall utgår uppgiftskonstruktören från att sammanhanget är tydligt nog att det inte behöver definieras att det är en matematisk kurva som efterfrågas, men hur tydligt ett sammanhang är beror självklart på vem som läser texten. :)
Jag vet att matematisk kurva förklaras i både Matematik 5000 1c och 2c då en bekant som läste på komvux hade samma funderingar. Jag har inte dessa tillgängliga och mitt lärarkonto har gått ut på Natur & Kultur. Jag kan kanske kolla biblioteket imorgon för att "bevisa" Skafts teori.
Tyvärr så är det väl ofta så på gymnasienivå att eleverna förväntas ha en omedelbar intuitiv förståelse av vad olika begrepp betyder. En formell matematisk definition av en kurva, som den jag nämnde i ett tidigare inlägg (från Wikipedia), kräver ju begrepp (kontinuitet, bild, funktion, topologi…) som inte rimligen kan förstås av en gymnasieelev.
Tyckte själv att det var lite jobbigt i gymnasiet att man förväntades ha en intuitiv insikt i olika begrepp utan en tydlig formell grund (tex vad det gäller gränsvärden, asymptoter, integraler etc.). Det var ju märkligt nog nästan lättare att läsa matte på universitetsnivå då olika begrepp fick en tydlig definition som man sedan kunde falla tillbaka på.
Med det sagt, så finns det ju ytterligare ett begrepp i frågan som vi förväntas ha en intuitiv känsla för; nämligen begreppet tangent. Vad innebär det att två kurvor tangerar varandra? Jag tror alla har en intuitiv geometrisk känsla för vad detta innebär, men hur många kan ställa upp en formell definition av vad det innebär ”att tangera”? Det är verkligen svårt att hitta läroböcker som formellt definierar detta begrepp - själv har jag bara kommit i kontakt med en enda bok som gett en matematiskt rigorös definition av vad som avses med ”att tangera”.
Ett annat exempel på ett ord som betyder en sak i vardagsspråket och en annan inom sitt fack: En botanist anser att en banan är ett bär men att en jordgubbe inte är det (en jordgubbe är en stenfrukt).
Tillägg: eller som min (kemi)elev som svarade på historiefrågan om vad "reduktionen" (på Gustav II Adolfs tid) innebar med att svamla om elektroner...
Smaragdalena skrev:Ett annat exempel på ett ord som betyder en sak i vardagsspråket och en annan inom sitt fack: En botanist anser att en banan är ett bär men att en jordgubbe inte är det (en jordgubbe är en stenfrukt).
Jordgubben är en skenfrukt—inte en stenfrukt. :) Däremot är det många "nötter" som egentligen är stenfrukter (jordnöt, valnöt, cashew, kokosnöt, mandel...)
Felskrivning... tack! Körsbär och plommon är väl stenfrukter?
Smaragdalena skrev:Felskrivning... tack! Körsbär och plommon är väl stenfrukter?
Du verkar ha helt rätt.
Ja, då har jag fått fel uppfattning av specifik definition för en kurva inom matematik.
@PATENTERAMERA - Håller med dig.
Smaragdalena skrev:Ett annat exempel på ett ord som betyder en sak i vardagsspråket och en annan inom sitt fack: En botanist anser att en banan är ett bär men att en jordgubbe inte är det (en jordgubbe är en stenfrukt).
Tillägg: eller som min (kemi)elev som svarade på historiefrågan om vad "reduktionen" (på Gustav II Adolfs tid) innebar med att svamla om elektroner...
Termen frukt i sig är ju intressant, eftersom användningen i folkmun är striktare än användningen inom naturvetenskap, lite som att palindrom ofta ses som ett ord som är likadant fram- och baklänges, men som egentligen bara ska vara något ord framlänges, och något ord baklänges. Annars är nog motsatsen vanligare – energi, kraft, kurva, tvål, bakterier/virus (används tyvärr ofta helt fel), penicillin, m.fl. – men inte frukt! Något trevligt att fundera på såhär på kvällskvisten. :)









