Täthetsfunktion

Kan det här vara på rätt spår?

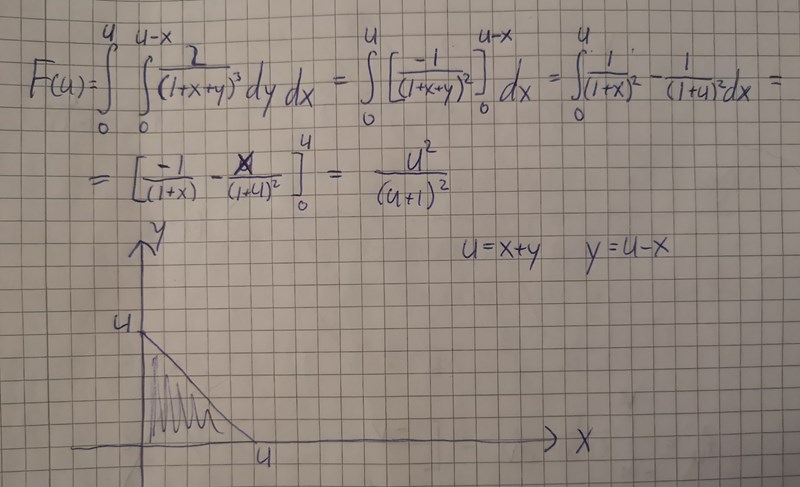
Tack, det ser korrekt ut! Kanske ett bättre sätt än att gå via en transformation? Även om jag tycker det borde fungera också.

Micimacko, hur blir motsvarande integral på b-uppgiften? 🤔

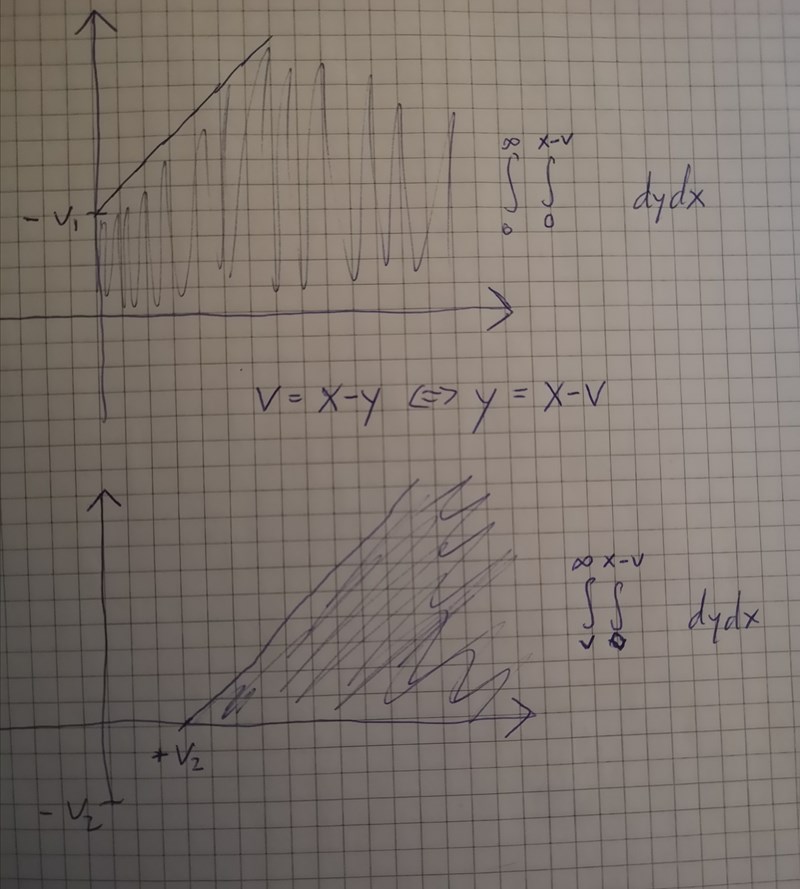Något sånt på b kanske? Jag försökte också med transformation först men fick inte fram något vettigt alls. Lyckades inte hitta satsen beskriven heller, men har för mig att det ställer en del krav på funktionerna så hade börjat med att kolla om det ska vara möjligt.

Hej Micimacko!

Jag fick något liknande, men tyckte det var lurigt med begränsningen att $x,y>0$. Denna integral fick jag:

$\displaystyle F_V(v)=P(V\le v)=P(X-Y\le v)=$

$\displaystyle \int_0^{\infty} \int_0^{\max(y+v;0)}\frac{2}{(1+x+y)^3}dxdy$

Tycker det är lite svårt att veta hur jag ska hantera max-villkoret.

Tror man åker på falluppdelning. Jag undvek att integrera x först för att slippa 2 integraler i ena fallet. Men jag har nog tagit fel sida av linjen.

Micimacko skrev:

Tror man åker på falluppdelning. Jag undvek att integrera x först för att slippa 2 integraler i ena fallet. Men jag har nog tagit fel sida av linjen.

Jag fattar. Det bör ju gälla att $f_V(v)=f_V(-v)$ av symmetriskäl, så jag är inne på att man kunde göra beräkningarna endast för $v\ge 0$, då slipper man dela upp det i två integraler.

Hej!

När du hittat $f_{U,V}(u,v)$ så kan du hitta de marginella täthetsfunktionerna genom att integrera $f_{U,V}(u,v)$ "över alla möjliga värden på den icke intressanta variabeln". Exempelvis har du 

$f_{U}\left(u\right)=\displaystyle \int_{\Omega}f_{U,V}\left(u,v\right)dv$ där $v\in \Omega$. 

Tack Moffen!

Jag försökte lösa det på det sättet, men visste inte hur jag skulle sätta upp integralerna.

Vad blir $\Omega$ i a) resp. b)?

tomast80 skrev:

Tack Moffen!

Jag försökte lösa det på det sättet, men visste inte hur jag skulle sätta upp integralerna.

Vad blir $\Omega$ i a) resp. b)?

Hej!

a)

Om jag kommer ihåg rätt bör det vara värdemängden för funktionen $f\left(x,y\right)=x-y$, dvs. typ ditt $V$.

I ditt fall bör det därför bli $\Omega_{V}=\{x\in\mathbb{R}\text{ : } -\infty<x<+\infty\}$ med tanke på att $x,y>0$ så deras differens kan anta alla olika värden.

b)

På samma sätt, men nu integrerar vi $f_{U,V}\left(u,x\right)$ med avseende på $u$. Funktionen $f\left(x,y\right)=x+y$ bör ha värdemängd $\Omega_{U}=\{x\in\mathbb{R}\text{ : } 0<x<+\infty\}$.

Testa gärna om det ger rätt resultat, jag har inte dubbelkollat och minnet kanske sviker, men jag har för mig att man kan göra så...

EDIT: Formellt har du såklart att du integrerar från $-\infty$ till $+\infty$, men att utanför gränserna ovan så gäller inte längre $f_{U,V}\left(u,v\right)$, utan man "antar" bara att den är lika med $0$ utanför det givna intervallet. Mer korrekt är att alltid specificera för vilka $u$ och $v$ som $f_{U,V}\left(u,v\right)$ gäller och definiera den som $0$ annars.

Tack Moffen!

Jag misstänker att jag fått fram fel funktion:

$f_{U,V}(u,v)$
Den beror inte ens av $v$ så när jag integrerar över den variabeln blir det en divergent integral.

Sannolikt har jag gjort fel i något tidigare steg... 🤔

Så här långt kom jag:

Det som blir grisigt här är ju att den där tätheten inte gäller överallt, eller rättare sagt att definitionsområdet inte är rektangulärt. Som Moffen säger är kan u anta alla positiva värden, och v alla reella värden. Men 

$f_{u,v}(3,-5)=0$

likafullt. Så tätheten beror faktiskt v, på så sätt att v bestämmer inom vilka gränser tätheten är nollskild. För ett fixt u bör v kunna variera från -u till u. Så marginella tätheten för u bör vara:

${\int }_{-u}^u\frac{1}{{(1+u)}^3}dv=\frac{2u}{{(1+u)}^3}$

vilket stämmer med den fördelningsfunktion Mickimacko fick i post 2.

Problemet är att med v så får vi ändå samma fula falluppdelning: om v är positivt bör u kunna variera från v till oändlighten, men om v är negativt kan u variera från -v till oändligheten om jag inte tänker fel (om v är negativt är -v=y-x positivt och u=x+y>y-x).

Så Moffens metod är principiellt den bästa men faller inte ut särskilt elegant i det här fallet. Om jag inte missat något.

Alltså definitionsområdet är skärningen mellan u>0 och u+v>0. 

Så nu kanske jag är övertydlig men tätheten är alltså:

$f_{u,v}(u,v)=\frac{1}{{(1+u)}^3}om u>0 och u+v>0$

och 0 annars.

Som för att illustrera att det här är lite grisigt har ju även jag lyckats glömma ett villkor: det måste ju också gälla att u>v.

Det sätt man borde löst den här uppgiften på är att konstatera att funktionen

U=X+Y

V=X-Y

i matrisform är en rotationsmatris, 45 grader medurs, så första kvadranten avbildas på en triangel med spets i origo och sidor v=u och v=-u.

Stort tack Smutsmunnen!

Enligt facit gäller att:

$\displaystyle f_V(v)=\frac{1}{2(1+|v|)^2}$

Ja men precis jag var lite trött och förvirrad igår och fick det att låta som att det var superavancerat när jag skrev:

"Problemet är att med v så får vi ändå samma fula falluppdelning: om v är positivt bör u kunna variera från v till oändlighten, men om v är negativt kan u variera från -v till oändligheten "

men det är ju inte mer komplicerat än att u kan variera från |v| till oändligheten.

Smutsmunnen skrev:

Ja men precis jag var lite trött och förvirrad igår och fick det att låta som att det var superavancerat när jag skrev:

"Problemet är att med v så får vi ändå samma fula falluppdelning: om v är positivt bör u kunna variera från v till oändlighten, men om v är negativt kan u variera från -v till oändligheten "

men det är ju inte mer komplicerat än att u kan variera från |v| till oändligheten.

Snyggt! Tack för hjälpen!