Teckna ett rationellt uttryck för antal timmar som hon jobbat under 2 mån.
hej.
vet inte var jag ska börja.. behöver tips.

mvh
Här kan det vara bra att börja "baklänges".
Sätt T = totala antalet timmar Johanna har jobbat under januari och februari.
Om J är antalet timmar Johanna arbetade i januari och F är antalet timmar hon arbetade i februari så får du att T = J+F.
Nästa steg blir då att ta fram uttryck för J och F.
Gör ett försök och visa hur det går.
Yngve skrev:Här kan det vara bra att börja "baklänges".
Sätt T = totala antalet timmar Johanna har jobbat under januari och februari.
Om J är antalet timmar Johanna arbetade i januari och F är antalet timmar hon arbetade i februari så får du att T = J+F.
Nästa steg blir då att ta fram uttryck för J och F.
Gör ett försök och visa hur det går.
Det här får jag till att börja med.
OK, kan du nu med hjälp av det gulmarkerade ta fram ett uttryck för J och med hjälp av det blåmarkerade ta fram ett uttryck för F?

(De båda uttrycken ska innehålla x och siffror.)
Yngve skrev:OK, kan du nu med hjälp av det gulmarkerade ta fram ett uttryck för J och med hjälp av det blåmarkerade ta fram ett uttryck för F?
(De båda uttrycken ska innehålla x och siffror.)
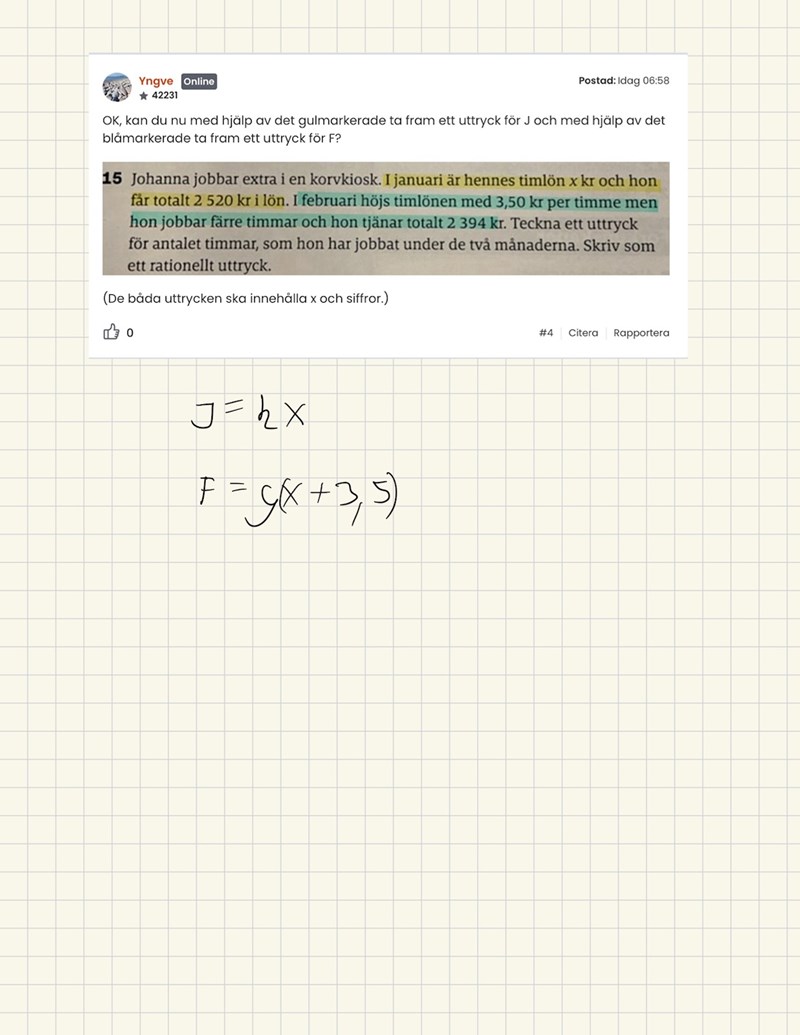
Nej, det var inte så jag menade.
=========
Är du med på följande?
Om Johanna jobbar J timmar i januari med timlönen x kronor per timme så får Johanna ut J*x kronor i lön (dvs den totala lönen är antalet arbetade timmar multiplicerat med timlönen).
Vi vet att Johanna får ut 2 520 kronor i januari.
Alltså måste det gälla att J*x = 2 520 kronor.
Om du nu dividerar med x på båda sidor å får.du att J = 2 520/x.
Det var detta jag menade med "ett uttryck flr J som endast innehåller x och siffror".
Yngve skrev:Nej, det var inte så jag menade.
=========
Är du med på följande?
Om Johanna jobbar J timmar i januari med timlönen x kronor per timme så får Johanna ut J*x kronor i lön (dvs den totala lönen är antalet arbetade timmar multiplicerat med timlönen).
Vi vet att Johanna får ut 2 520 kronor i januari.
Alltså måste det gälla att J*x = 2 520 kronor.
Om du nu dividerar med x på båda sidor å får.du att J = 2 520/x.
Det var detta jag menade med "ett uttryck flr J som endast innehåller x och siffror".
Hm.. det liknar ju det jag ställt upp först i mitt första svar. Hajar. Så jag fortsätter därifrån och ser om jag lyckas utveckla det enligt samma mönster
Yngve skrev:Nej, det var inte så jag menade.
=========
Är du med på följande?
Om Johanna jobbar J timmar i januari med timlönen x kronor per timme så får Johanna ut J*x kronor i lön (dvs den totala lönen är antalet arbetade timmar multiplicerat med timlönen).
Vi vet att Johanna får ut 2 520 kronor i januari.
Alltså måste det gälla att J*x = 2 520 kronor.
Om du nu dividerar med x på båda sidor å får.du att J = 2 520/x.
Det var detta jag menade med "ett uttryck flr J som endast innehåller x och siffror".
Såhär gjorde jag och såhär står det i facit. Vad tycker du?

Ditt svar är en ekvation, inte ett uttryck.
========
Det är rätt att J = 2520/x, men sedan har du hoppat över steget att ta fram ett uttryck för F.
Det kan du göra på samma sätt som du gjorde för J, nämligen:
F*(X+3,5) = 2394, vilket betyder att F = 2394/(x+3,5).
=======
Du har alltså att J = 2520/x och att F = 2394/(x+3,5).
Sista steget blir nu att ta fram ett uttryck för J+F.
Yngve skrev:Ditt svar är en ekvation, inte ett uttryck.
========
Det är rätt att J = 2520/x, men sedan har du hoppat över steget att ta fram ett uttryck för F.
Det kan du göra på samma sätt som du gjorde för J, nämligen:
F*(X+3,5) = 2394, vilket betyder att F = 2394/(x+3,5).
=======
Du har alltså att J = 2520/x och att F = 2394/(x+3,5).
Sista steget blir nu att ta fram ett uttryck för J+F.
Wow, riktigt spännande uppgift. Förstod inte att man fick dela upp det i flera steg genom J + F sen, så lärorikt exempel.
tack för tålamodet Yngve även om mitt tålamod också är imponerande med tanke på att jag fastnar i sånt här dag in dag ut😅. 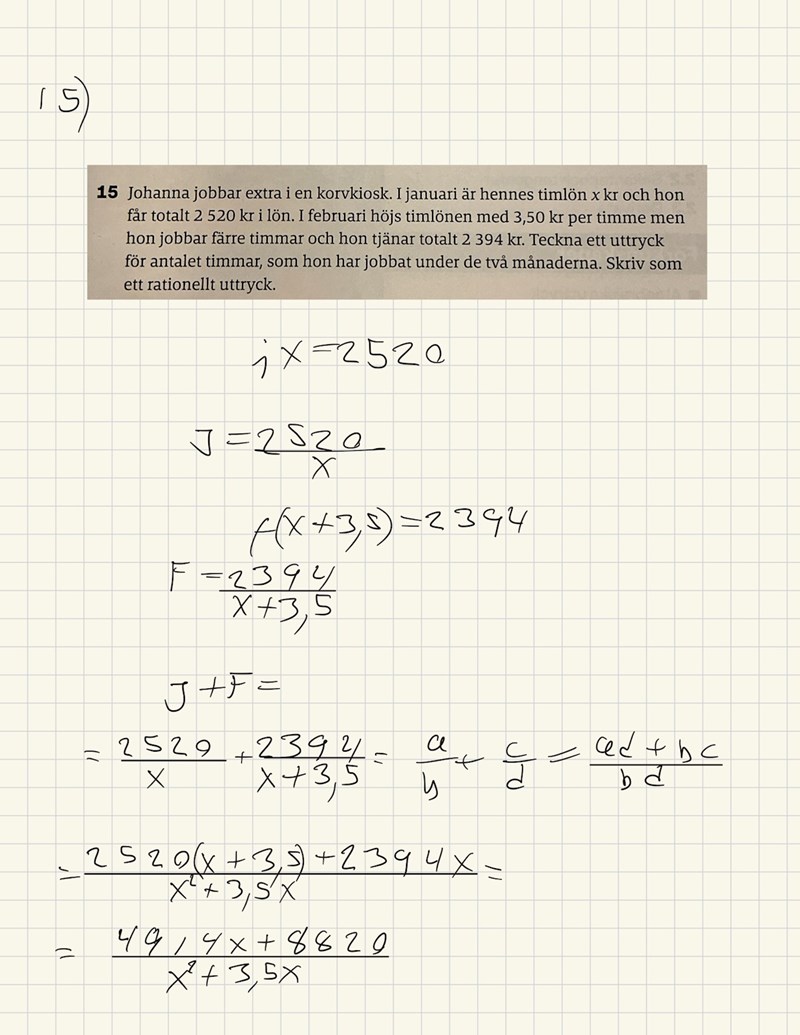
Bravo!
Det märks att du har koll på uträkningarna, så i det här fallet var det svåra "bara" att tolka uppgiften och bryta ner den till enklare delar (det jag pratade om i början, nämligen "baklänges"-tänket).
Yngve skrev:Bravo!
Det märks att du har koll på uträkningarna, så i det här fallet var det svåra "bara" att tolka uppgiften och bryta ner den till enklare delar (det jag pratade om i början, nämligen "baklänges"-tänket).
Har det i åtanke. Trevlig helg!



