Teckna områdets area mhs integraler
Ska jag börja med att hitta nollställen för båda funktinerna, sedan antideriverar jag dem och sätter övre och undre gräns ?
Med antiderivatan är du på väg att beräkna arean och det behöver du inte. Det räcker med att teckna de båda integralerna. De gemensamma punkterna däremot behövero du.
Tomten skrev:Med antiderivatan är du på väg att beräkna arean och det behöver du inte. Det räcker med att teckna de båda integralerna. De gemensamma punkterna däremot behövero du.
Hur hittar jag dem ?
1. Sätt 4/x2 =4/x och lös den ekv. Det är där de båda kurvorna skär varandra.
2. Sätt 4/x2 =1. Och lös den ekv.. Det är där kurvan y= 4/x2 skär linjen y=1
Kan inte jag döpa en funktion till y1 och den andra till y2. Jag hittar rööterna när y1=y2.
De intressanta punkterna kan du avläsa i diagrammet, du behöver inte räkna ut dom!
I den här uppgiften har du nytta av formeln för beräkning av "area mellan grafer", som jag beskrev i en av dina andra trådar.
 Man kan se det som att den sökta arean är skillnaden mellan areorna i figuren, d v s skillnaden mellan integralerna. (OBS! att man då får subtrahera en etta.) Man behöver inte räkna ut dem, även om de är "elementära".
Man kan se det som att den sökta arean är skillnaden mellan areorna i figuren, d v s skillnaden mellan integralerna. (OBS! att man då får subtrahera en etta.) Man behöver inte räkna ut dem, även om de är "elementära".
Uppgiften är nog tänkt att pröva förståelsen för den geometriska tolkningen av begreppet integral

Varför ska man subtrahera en etta ?
Arup skrev:
Varför ska man subtrahera en etta ?
Arean av de markerade områdena ges av respektive , eftersom "undre" funktionen i båda fallen är .
Det är alltså tillämpningar av formeln för beräkning av area mellan grafer, nämligen Area = Integralen av ("övre" funktionen minus "undre" funktionen).
Ett annat (och inte lika stiligt) sätt att beräkna arean är
Kan du markera i bilden vilka områden som respektive integral anger arean för?
Löste på skoj. Jag tänkte som Yngve. Hittade även uppgiften med facit på nätet. Där ville man ha den ”inte lika stiliga” lösningen. Lite märkligt, eftersom det blir mer komplicerat att göra så, särskilt om man skall integrera för att faktiskt beräkna arean.
Den elegantare lösningen är inte min utan hansas (svar #9).
Yngve skrev:Den elegantare lösningen är inte min utan hansas (svar #9).
Där ser man. Läste inte hela tråden. Bra du rättar.
eller så kan man 'skoja till det'...
Kan man göra så hör ?

Nej, det stämmer inte.
Integralen du sätter upp som y1 ger följande area:

Integralen du sätter upp som y2 ger dig följande area:

Summan av dessa areor är inte lika med det som efterfrågas.
Ett annat fel är detta:

Denna likhet gäller inte.
Är du med på dessa tre viktiga saker?
Yngve skrev:Är du med på dessa tre viktiga saker?
ja, men jag förstod dock inte varför man skullle subtrahera en etta
Eftersom Yngve är offline.
När du använder integraler för att beräkna en area så är det mellan två funktioner, ∫(f(x)-g(x)) dx.
Skall arean vara med x-axeln som bas är den andra funktionen g(x)=0.
Det är dock rätt onödigt att integrera f(x)-0 dx, så man skippar g(x) förstås.
Nu vill du ha arean under kurvan, men inte ned till x-axeln. Du vill ha den över linjen y=1. Då blir det ∫ (f(x)-1) dx.
Rimligt?
Jag förstpr inte vsrför man integrerar Int[f(x)-1]dx och inte Int[f(x)] dx ?
Det vi gör när vi subtraherar 1 är att essentiellt flytta ned allting en enhet. Är du med på att det gröna området har samma area i båda dessa bilder?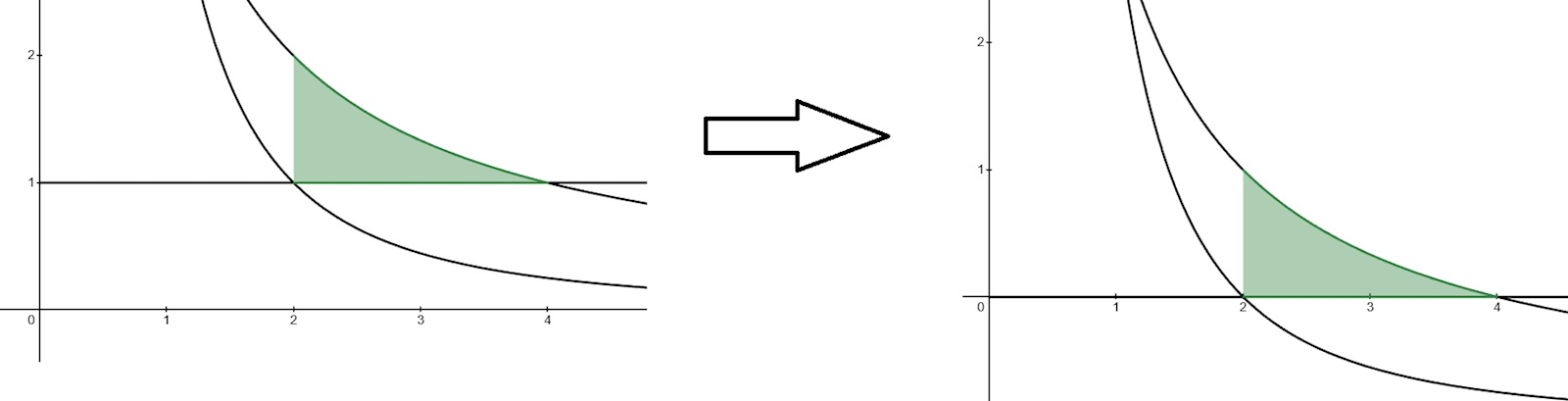
Arup skrev:Jag förstpr inte vsrför man integrerar Int[f(x)-1]dx och inte Int[f(x)] dx ?
Jag gör en kompletterande illustration av skillnaden.
- Integralen ger dig den blåmarkerade arean i denna bild. Detta eftersom arean som då beräknas ligger mellan kurvan y = 4/x och linjen y = 0.

- Integralen ger dig den blåmarkerade arean i denna bild. Detta eftersom arean som då beräknas ligger mellan kurvan y = 4/x och linjen y = 1.

=======
Var det svar på din fråga eller var det något annat du menade?
ja
OK bra.
Är du även med på att den efterfrågade arean kan beräknas som A1-A2?


ja, det är logiskt
OK bra.
Har du några ytterligare frågor specifikt rörande den här uppgiften?
Kanske hur jag ställa upp integral uttrycken.
Arup skrev:Kanske hur jag ställa upp integral uttrycken.
Kolla svar #11
Yngve skrev:Arup skrev:Kanske hur jag ställa upp integral uttrycken.
Kolla svar #11
Nu kanske mitt svar #21 är lättare att greppa också. Du har alltid en g(x), mitt exempel, när du integrerar för en area. Det är bara det att den oftast är =0 när man börjar lära sig, så man glömmer den.
Tillägg: 11 jan 2026 22:36
Tips till TS alltså, när Yngve förklarat så bra.
sictransit skrev:
Nu kanske mitt svar #21 är lättare att greppa också. Du har alltid en g(x), mitt exempel, när du integrerar för en area. Det är bara det att den oftast är =0 när man börjar lära sig, så man glömmer den.
Jag ser inte vad skillnaden är?
i svar #12 hittade du ett alternativ lösning nämligen:
Jag undrar hur det hänger ihop med det du skrev i #11 :
Arup skrev:i svar #12 hittade du ett alternativ lösning nämligen:
Jag undrar hur det hänger ihop med det du skrev i #11 :
Det är två olika sätt att beräkna den efterfrågade arean.
=======
Att förstå hur ett integraluttryck kopplar till en area är en grundförutsättning för att kunna lösa denna och liknande uppgifter.
För att du ska få tröna på detta, (och för att vi ska kunna bli säkra på att du har förstått hur det hänger ihop) så föreslår jag att du gör 4 skisser, där du för var och en av de fyra nämnda integralerna grafiskt illustrerar vilken area de motsvarar.
Utgå då från denna bild:

Kopiera den i fyra exemplar och för var och en av dessa: Markerar området vars area motsvaras av:
Jag vet inte om jag har gjort rätt

Jag har problem med att rita ut I3 och I4
Arup skrev:Jag vet inte om jag har gjort rätt
Det här stämmer bra.
Arup skrev:
Det här stämmer inte.
Integralen beskriver att området går från x = 2 till x = 4, att den övre funktionen är y = 4/x och att den undre funktionen är y = 1.
Men det område du har markerat går från x = 1 till x = 2, den övre funktionen är y = 4/x2 och den undre funktionen är y = 1.
=======
Behöver du hjälp med att gå metodiskt tillväga för att koppla integraluttryck till grafer och områden?
Ja
OK, vi kan börja med denna:

Vi ser att
- Områdets vänstra gräns är x = 1, alltså ska integralens undre gräns vara 1.
- Områdets högra gräns är x = 4, alltså ska integralens övre gräns vara 4.
- Områdets övre gräns utgörs av grafen till funktionen y = 4/x.
- Områdets undre gräns utgörs av x-axeln, dvs grafen till funktionen y = 0.
- Integranden ska vara "övre funktion" minus "undre funktion", vilket i detta fallet blir 4/x - 0, som kan skrivas 4/x.
- Sammantaget ger detta att områdets area kan beslrivas av
=========
Kan du nu göra exakt samma sak, dvs skriva ner och visa oss steg 1 till 6 för följande område?







