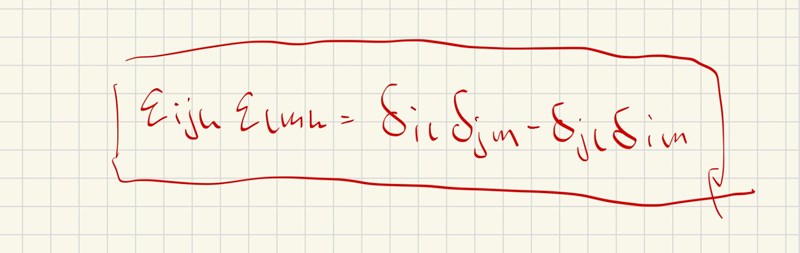Tensormetoder för att omforma följande uttryck

Hej!
Jag vet inte om det är tänkt att utnyttja indexräkning i uppg a-c)? Hur ska jag behandla A som jag inte vet om det är en tensor eller ett vektor?
Ja, använd indexräkning.
Fetstil = vektor. Vanlig stil = skalär.
PATENTERAMERA skrev:Ja, använd indexräkning.
Fetstil = vektor. Vanlig stil = skalär.
Aa ok. Jag får tyvärr inte som facit i b) uppgiften. Jag vet inte vad som gått snett.
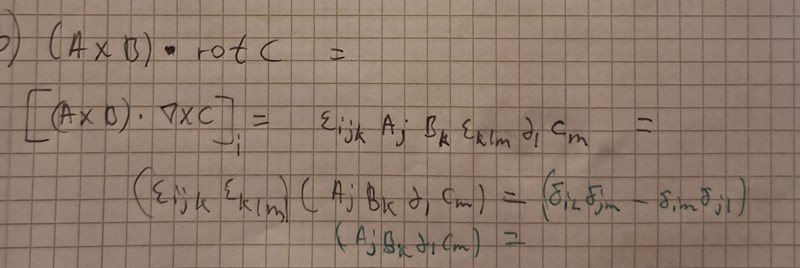

Tänk på att du har en skalärprodukt. Resultatet skall bli en skalär.
(AxB)i(rotC)i.
PATENTERAMERA skrev:Tänk på att du har en skalärprodukt. Resultatet skall bli en skalär.
(AxB)i(rotC)i.
Ja det är jag med på. Men varför ska båda termerna ha en i?
Därför att du har en skalärprodukt. v•u = viui.
PATENTERAMERA skrev:Därför att du har en skalärprodukt. v•u = viui.
Så då ska man göra på det sättet?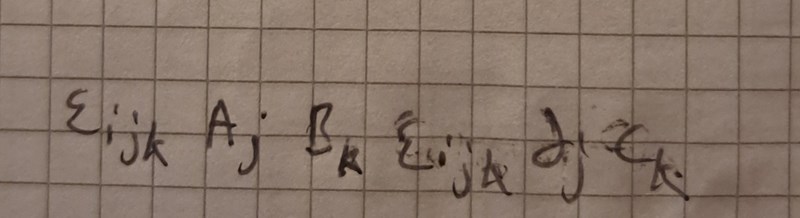
Ett dummyindex får bara förekomma 2 gånger, så du får använda lite fler bokstäver.
PATENTERAMERA skrev:Ett dummyindex får bara förekomma 2 gånger, så du får använda lite fler bokstäver.
Men vad var felet med det jag gjorde innan? Då hade jag ju eijkAjBkeklmdlCk
Du hade ett fritt index i, men i en skalär så finns inga fria index.
PATENTERAMERA skrev:Du hade ett fritt index i, men i en skalär så finns inga fria index.
Ja ok. Det missade jag! Men då kan man isåfall välja eilm
Ja, tex eilm och eijk.
PATENTERAMERA skrev:Ja, tex eilm och eijk.
Jag vill använda det här sambandet nedan för att skriva om eijkeilm men vet ej hur man kan göra det systematiskt.

Jag kom fram till följande uttryck , men varför är det inte tillåtet att omvandla diCm till kroneckerdeltaim? Svaret blir ju 0 dvs en skalär, men antar att man inte ska visa det steget.
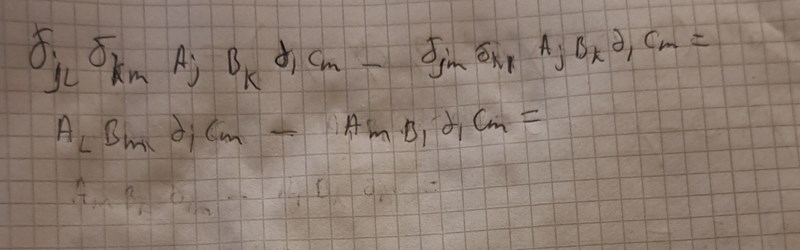
destiny99 skrev:Jag kom fram till följande uttryck , men varför är det inte tillåtet att omvandla diCm till kroneckerdeltaim? Svaret blir ju 0 dvs en skalär, men antar att man inte ska visa det steget.
Ja, något sådant vekar det bli. Vad säger facit?
Du kan skriva det som B•(A•)C - A•(B•)C.
PATENTERAMERA skrev:Du kan skriva det som B•(A•)C - A•(B•)C.
Ja precis det fick jag också. Samma svar som facit