Tensortransformation A till ett koordinatsystem K' med en vinkel alfa kring z axeln

Ja du har förstått det korrekt, $i$ är index för raderna och $k$ är index för kolumnerna i $A_{ik}$. På samma sätt gäller det för $B_{kj}$.

Eftersom uttrycket $A_{ik}B_{kj}$ har ett gemensamt index $k$  ska "matriserna" multipliceras. Man säger att tensorprodukten ska kontraheras över index $k$ 

Det finns 

D4NIEL skrev:

Ja du har förstått det korrekt, $i$ är index för raderna och $k$ är index för kolumnerna i $A_{ik}$. På samma sätt gäller det för $B_{kj}$.

Eftersom uttrycket $A_{ik}B_{kj}$ har ett gemensamt index $k$  ska "matriserna" multipliceras. Man säger att tensorprodukten ska kontraheras över index $k$ 

Det finns 

Vad innebär det att tensorprodukten kontraheras över index k? Vad står den där mitten matrisen för ?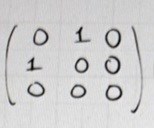

Det är tensorns komponenter i det oprimmade koordinatsystemet - sammanfattade som en matris.

Kontraktion innebär att två index sätts lika och implicerar en summering över dessa index.

PATENTERAMERA skrev:

Det är tensorns komponenter i det oprimmade koordinatsystemet - sammanfattade som en matris.

Kontraktion innebär att två index sätts lika och implicerar en summering över dessa index.

I det oprimmade systemet har vi ( ex, ey och ez)? Det är konstigt att sista kolonnen inte är ez (0,0,1) utan bara (0,0,0). Hur fick man till den ?

Så om vi A_ikB_kj , vad är det som kontraheras och vilka index sätts lika mee varandra?

Andra indexet på A sätts lika med första indexet på B (båda lika med k).

destiny99 skrev:

PATENTERAMERA skrev:

Det är tensorns komponenter i det oprimmade koordinatsystemet - sammanfattade som en matris.

Kontraktion innebär att två index sätts lika och implicerar en summering över dessa index.

I det oprimmade systemet har vi ( ex, ey och ez)? Det är konstigt att sista kolonnen inte är ez (0,0,1) utan bara (0,0,0). Hur fick man till den ?

Så om vi A_ikB_kj , vad är det som kontraheras och vilka index sätts lika mee varandra?

Du måste fått tensorn A_ij given på något sätt. Den behöver inte förhålla sig till basvektorerna på något speciellt sätt.

PATENTERAMERA skrev:

destiny99 skrev:

Visa föregående citat

PATENTERAMERA skrev:

Det är tensorns komponenter i det oprimmade koordinatsystemet - sammanfattade som en matris.

Kontraktion innebär att två index sätts lika och implicerar en summering över dessa index.

I det oprimmade systemet har vi ( ex, ey och ez)? Det är konstigt att sista kolonnen inte är ez (0,0,1) utan bara (0,0,0). Hur fick man till den ?

Så om vi A_ikB_kj , vad är det som kontraheras och vilka index sätts lika mee varandra?

Du måste fått tensorn A_ij given på något sätt. Den behöver inte förhålla sig till basvektorerna på något speciellt sätt.

Ja juste. Såhär står det på mina anteckningar

Men jag antar att tensorn A_ij alltid är givet på det sättet när man ska skriva på matrisform.

PATENTERAMERA skrev:

Andra indexet på A sätts lika med första indexet på B (båda lika med k).

Ok. Det innebär alltså att man behöver transponera B för att det ska se ut som A_ikB^T_kj och då är första index i A lika med första index i B efter transponering? 

Ja, för att skriva det med normala matrisprodukter så transponerar man.

Övning: Om (A’_ij) = $\left(\begin{array}{ccc}0& 1& 0\\ 1& 0& 0\\ 0& 0& 0\end{array}\right)$, vad bir då (A_ij)?

PATENTERAMERA skrev:

Ja, för att skriva det med normala matrisprodukter så transponerar man.

Övning: Om (A’_ij) = $\left(\begin{array}{ccc}0& 1& 0\\ 1& 0& 0\\ 0& 0& 0\end{array}\right)$, vad bir då (A_ij)?

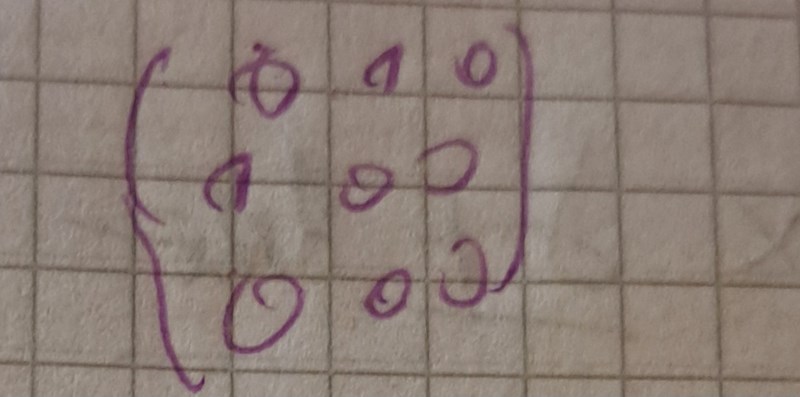
Nja, hur kom du fram till det?

PATENTERAMERA skrev:

Nja, hur kom du fram till det?

Jag tänkte transponatet av det du hade A_ij' för att få A_ijmen jag kanske ha tolkat detta helt fel. Annars vet jag tyvärr inte hur det ska vara.  Frågan är vad A_ij' ens är för något? Det verkar vara lik matrisen i #8

 A’_ij är tensorns komponenter i det primmade systemet. A_ij är tensorns komponenter i det oprimmade. I uppgiften fick du en tensors komponenter i det oprimmade systemet och skulle räkna ut dess komponenter i det primmade. Nu fick du en tensors komponenter i det primmade systemet och uppgiften var att räkna ut dess komponenter i det oprimmade.

PATENTERAMERA skrev:

 A’_ij är tensorns komponenter i det primmade systemet. A_ij är tensorns komponenter i det oprimmade. I uppgiften fick du en tensors komponenter i det oprimmade systemet och skulle räkna ut dess komponenter i det primmade. Nu fick du en tensors komponenter i det primmade systemet och uppgiften var att räkna ut dess komponenter i det oprimmade.

Aa ok.

D4NIEL skrev:

Tack! Det misset såg jag inte.

Löste du uppgiften?

Som förberedelse kan du visa att ${\Lambda }_{ik}{\Lambda }_{jk }={\Lambda }_{ki}{\Lambda }_{kj}={\delta }_{ij}$.

PATENTERAMERA skrev:

Löste du uppgiften?

Som förberedelse kan du visa att ${\Lambda }_{ik}{\Lambda }_{jk }={\Lambda }_{ki}{\Lambda }_{kj}={\delta }_{ij}$.

Nej jag löste inte då frågan var utanför detta inlägg.   Jag återkommer med ett nytt inlägg som vanligt om jag kör fast på en uppgift  som har med detta att göra. Det lär ta ett tag tills jag är van med detta.