Tetraeder problem

För a), jag ser några saker. För den första det är en regelbundet tetraeder, dvs att alla vinklar är . För den andra ser jag att jag kan ta $$höjden = z - Proj_{x,y} z$$.
Men därifrån vet jag inte.
Som i filmen 6th sense. I can see some dead people, men hur ska man fixa deras problem liksom....
Jag tror att jag skulle börja med att placera in tetraedern i ett koordinatsystem (inskriven i en kub för att det gör det lättare för mig att tänka). Tetraederns hörn ligger i (0,0,0), (a,a,0), (a,0,a) respektive (0,a,a) där a kan beräknas med hjälp av Pythagoras sats, eftersom man vet att avståndet mellan två hörn är 1 längdenhet.
Av symmetri så kommer höjden att skära sidan som spänns av x och y längs vektorn (x + y). Om du projicerar z på (x + y) så bör det bli rätt. Då behöver du bara projicera på en vektor (och inte på två som inte heller är ortogonala).
Bygg en tetraeder av papper och tejp, om det är svårt att föreställa sig den i huvudet.
Ta ett gammalt kuvert, klipp av ena kortsidan och platta till det på andra hållet. Jag är så lättroad att jag tycker det är fascinerande att man kan göra en tetraeder på detta sätt.
En gång såg jag en film om hur man fyllde i mjölk i tetrapak på 60-talet - man hade ett plasttäckt kartongflak som var böjt som ett U runt röret där mjölken fylldes på, förenade kartongen till ett rör, klämde ihop röret så att det blev platt, fyllde i mjölken, * klämde ihop röret vinkelrätt mot det förra vecket så att det skapades två fogar, klippte av mellan tetrorna, fyllde på mjölk i nästa tetra, upprepa från *. Man kunde alltså skapa en kontinuerlig process för att fylla förpackningarna.
Just att föreställa mig en tetraeder i 3D är det inga problem -pga mycket spelande förut bland annat, men det vore en lång (och ointressant) story :D
Däremot, projektionen...
Om vi säger att vi projicerar på , får jag, felaktigt:
(Shoot, vad hände med min LaTex? Jag märkte inte det igår...)
Bra att 3D-visualiseringen fungerar. En normal pyramid och en tetraeder är inte samma sak, men det visste du säkert redan.
LaTeX tyckte förmodligen inte om ö:et. Testar:
Testar instruktionerna för ö i LaTeX-guiden:
OK, det funkar, men det blir för fult för att jag ska använda det.
dajamanté skrev:Däremot, projektionen...
Om vi säger att vi projicerar på , får jag, felaktigt:
Du projicerar här först på x och lägger sedan till projektionen på y. Det är inte samma sak som att projicera längs (x + y) när x och y inte är ortogonala.
Vad blir då
?
Laguna skrev:Bra att 3D-visualiseringen fungerar. En normal pyramid och en tetraeder är inte samma sak, men det visste du säkert redan.
LaTeX tyckte förmodligen inte om ö:et. Testar:
Testar instruktionerna för ö i LaTeX-guiden:
OK, det funkar, men det blir för fult för att jag ska använda det.
Själv tycker jag man får snyggast resultat om man skriver i textformat:
\text{ho}\"\text{jden}=z-\text{proj}_{x,y}\left(z\right)
Jag får nu .
Nu är jag ännu mer förvirrad än förut. Vad ska jag göra med dena vektorn igen?
Doktorn menar:
Du projicerar här först på x och lägger sedan till projektionen på y. Det är inte samma sak som att projicera längs (x + y) när x och y inte är ortogonala.
Vänta, jag trodde att när vektorer var inte ortogonala räckte det att normalisera projektionen? Annars var det:
?
(@Laguna och AlvinB : mycket stylisha skripturer!)
dajamanté skrev:
Vänta, jag trodde att när vektorer var inte ortogonala räckte det att normalisera projektionen? Annars var det:
?
Nej, om u1 och u2 delvis pekar åt samma håll (d.v.s inte är ortogonala) så blir det knas. Tänk att u1 = u2 . I så fall ger din formel ovan att projektionen av x i riktning u1 blir dubbelt så stor som den egentligen är.
Detta kan förenklas till...
Sorry för dröjsamt svar doktor. Det kan inte stämma i detta uppgift att u1 = u2, visst pratar vi om x och y axeln?
Precis, i detta fallet är u1 ≠ u2, men även att u1 och u2 inte är ortogonala (u1 och u2 är i ditt fall i den här uppgiften vektorerna x och y, eller hur?).
Jag tycker dock att det borde finnas en snyggare "helt vektorbaserad" lösning på uppgiften än det jag har kommit fram till. Skulle helst slippa behöva inse att projektionen är längs (x + y).
En annan variant är att införa en ON-bas och uttrycka vektorerna x, y och z i den basen. Vissa anser att det är "snyggare" att inte behöva införa en (ON-)bas för att lösa problem, men det är väl en smaksak.
Jag tycker också att det är snyggare att ha en "helt vektorbaserad" lösning som du kallar det, utan intermediära steg, men jag fortfarande fattar inte poängen, eller vad vi håller på med, eller även vad jag heter vid den här laget...
Om jag skriver
ser jag att vi närmar oss långsamt men säkert mot , men varför fick vi projektions formel av mot ? Varför blev det ?
I täljaren har jag använt att
x, y och z har alla längd 1, så skalärprodukterna blir bara cosinus av vinkeln mellan vektorerna.
Tack, beräkningsmässigt är jag typ med... Du menar att jag kan göra denna metod utan ON system?
Jag räknar helt utan någon specificerad bas!
Allt jag använder är att x, y och z har längd 1 och att vinklarna mellan två olika vektorer är 60°.
Jag använder sedan den vanliga euklidiska skalärprodukten och "insikten" att jag ska projicera z i riktninhen av (x + y).
är planet x + y = något konstant och z = 0 lika?
Det låter riktigt idiotisk men vi kunde inte avgöra det med en kompis. Alltså om x + y = konstant är vi kvar på x,y planet. Som bör vara samma som z = 0?
Nej det är inte samma plan. x+y=0 sätter ingen begränsning på z och planet z=0 sätter ingen begränsning på varken x eller y.
Ok, det behövs en fin illustration så att vi förstår varandra :)
Jag försöker fixa det senare idag.
uuhh tack.
Jag trodde att vid den här laget skulle allt Saint Emilion har evaporerats bort från hjärnblodkärl men kanske inte.
Här är en bild på en tetraeder med vektorerna x, y och z utritade. Projektionen av z i riktningen av (x + y) är utritad, liksom höjden mot sidan som spänns av x och y. Hjälper detta?
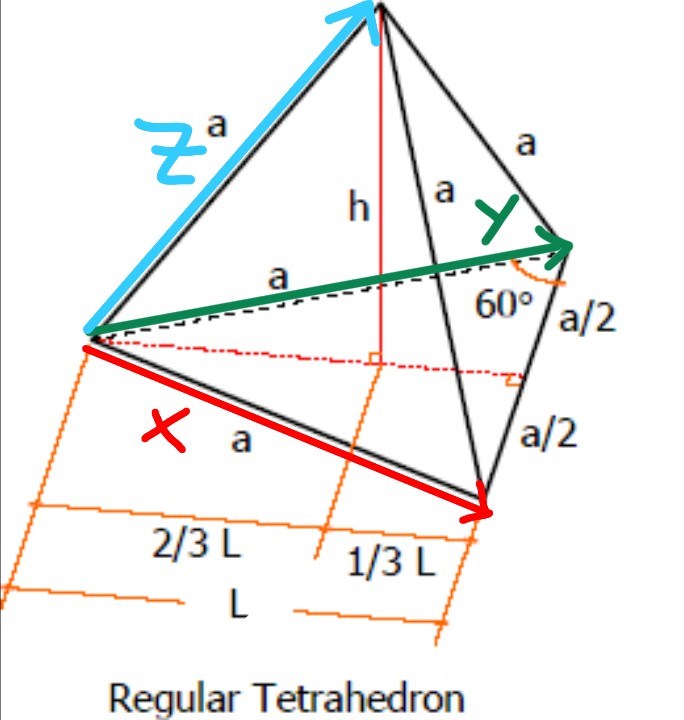
Jag det hjälper väldigt mycket.
Nu kommer du att tro att jag är insane (om du inte gör det redan), men jag måste klarifiera det innan tentan.
varför och inte ?
Finns det en skillnad mellan och i projektionsformel?
dajamanté skrev:Jag det hjälper väldigt mycket.
Nu kommer du att tro att jag är insane (om du inte gör det redan), men jag måste klarifiera det innan tentan.
varför och inte ?
Finns det en skillnad mellan och i projektionsformel?
Här är x och y inte ortogonala. Det gäller allmänt att
Med räkneregler för skalärprodukt kan det skrivas om som
Ser du nu vad som händer i ditt fall jämfört med det "vanliga" fallet där x och y är två ortogonala enhetsvektorer?
Ja, nu ser jag att jag får en promenerande rest av -som försvinner när vektorer som korsas är ortogonala. Tack Dr. G!
Bra!
Har du löst b)?
....
nej.
Är det ?
Har inte kollat.
Vad blir skalärprodukten av höjden med sig själv?
... jag räknade .
Är det också något begränsning för att höjden är inte ON-normerat mot sig själv??
Nu har du räknat som om x, y och z vore ortogonala!
Utveckla parenteserna med räknereglerna för skalärprodukt!







