Text till ekvation
Uppgift: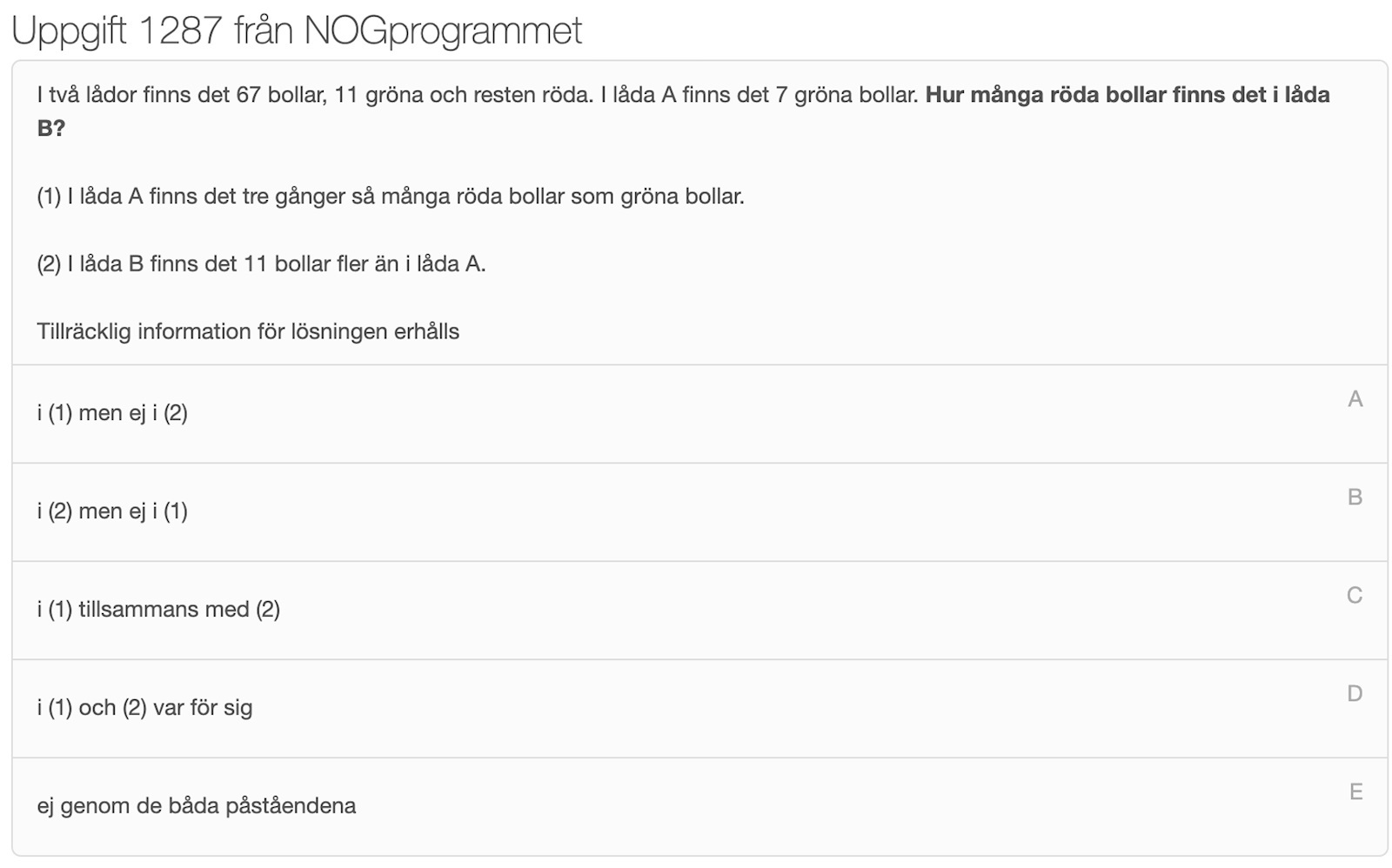 Lösning:
Lösning: Problem:
Problem:
varför skriver man in rb+4 och rb+7 när det är dem röda bollarna man söker? Hur ska man veta att man kan använda den informationen?
Du kan alltid använda all information, jag förstår inte riktigt din protest så som du formulerar den.
Du vet att du har två lådor A & B med röda och gröna bollar:
Sedan får du givet att du har totalt 67 bollar:
Sedan får du givet att det finns 11 gröna totalt:
Sedan får du givet att det finns 7 gröna i A:
Detta ger naturligtvis att:
Slutligen:
Frågan är dåligt ställd. Hur vet vi att det finns noll svarta bollar i låda A?
Bubo skrev:Frågan är dåligt ställd. Hur vet vi att det finns noll svarta bollar i låda A?
För att det finns 11 gröna och resten röda (56). Alltså inga svarta.
Ja, nu ser jag. Fel av mig.
Jag behöver nog en större skärm att läsa på.
Ebola skrev:Du kan alltid använda all information, jag förstår inte riktigt din protest så som du formulerar den.
Du vet att du har två lådor A & B med röda och gröna bollar:
Sedan får du givet att du har totalt 67 bollar:
Sedan får du givet att det finns 11 gröna totalt:
Sedan får du givet att det finns 7 gröna i A:
Detta ger naturligtvis att:
Slutligen:
Hej!
Förlåt jag hade nog svårt att formulera vad jag inte förstod. Jag förstod helt enkelt inte varför att ta med de gröna kulorna i ekvationen skulle hjälpa en i sökandet efter de röda!
Ett bra tips i sådana här uppgifter för att snabbt lösa dem är att räkna antalet ekvationer eller samband och antalet okända.
Du har 6 st okända:
I detta fallet börjar du med 5 st ekvationer. Varje påstående ger dig en extra ekvation. Därmed har du med (1) och (2) var för sig 6 st ekvationer och då kan du lösa problemet (bestäm ) med påstående (1) och (2) var för sig.


