The generalized plancherel identity

Jag vet ej om du har svaret men integralen är π/2 * 1 / (ab(a+b)) vilket ges genom part.uppdelning.

Jag kan tyvärr inte hjälpa till med "vägen dit" via Parseval då jag inte kommer ihåg mycket avs. komplex/linjär analys.

Trinity2 skrev:

Jag vet ej om du har svaret men integralen är π/2 * 1 / (ab(a+b)) vilket ges genom part.uppdelning.

Jag kan tyvärr inte hjälpa till med "vägen dit" via Parseval då jag inte kommer ihåg mycket avs. komplex/linjär analys.

Jo partialbråksuppdelning går absolut att lösa med denna uppgift. Men tror meningen är via parseval tyvärr.

destiny99 skrev:

Trinity2 skrev:

Jag vet ej om du har svaret men integralen är π/2 * 1 / (ab(a+b)) vilket ges genom part.uppdelning.

Jag kan tyvärr inte hjälpa till med "vägen dit" via Parseval då jag inte kommer ihåg mycket avs. komplex/linjär analys.

Jo partialbråksuppdelning går absolut att lösa med denna uppgift. Men tror meningen är via parseval tyvärr.

Var kommer 2π från? Är det inte denna

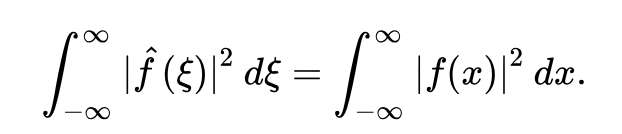
som avses. Men jag kan ha fel.

Vilket f har du och vad är f-hat?

Trinity2 skrev:

destiny99 skrev:

Visa föregående citat

Trinity2 skrev:

Jag vet ej om du har svaret men integralen är π/2 * 1 / (ab(a+b)) vilket ges genom part.uppdelning.

Jag kan tyvärr inte hjälpa till med "vägen dit" via Parseval då jag inte kommer ihåg mycket avs. komplex/linjär analys.

Jo partialbråksuppdelning går absolut att lösa med denna uppgift. Men tror meningen är via parseval tyvärr.

Var kommer 2π från? Är det inte denna

som avses. Men jag kan ha fel.

Vilket f har du och vad är f-hat?

Det är denna. Men jag är säker på att det ska stå en faktor 2pi framför andra integralen. Alltså fhatt är väl fouriertransformen av uppgiften och f(x) är väl integranden. 

Det finns en variant med två olika funktioner i. Det är nog den du skall använda.

Gjorde du inte en uppgift för att ta reda på Fouriertransformen till $\frac{1}{a^2+x^2}$? Det resultatet borde du kunna använda här.

PATENTERAMERA skrev:

Det finns en variant med två olika funktioner i. Det är nog den du skall använda.

Gjorde du inte en uppgift för att ta reda på Fouriertransformen till $\frac{1}{a^2+x^2}$? Det resultatet borde du kunna använda här.

Menar du dessa varianter? Vilken av de ska jag använda?

Hm fouriertransformen av 1/(a^2+x^2) är väl  e^-a|x|? Men jag tror inte jag har gjort fouriertransformen av 1/(a^2+x^2)

Den senare. Du har två funktioner där.

Du kan sätta f(x) = $\frac{1}{a^2+x^2}$ och g(x) = $\frac{1}{b^2+x^2}$.

PATENTERAMERA skrev:

Den senare. Du har två funktioner där.

Du kan sätta f(x) = $\frac{1}{a^2+x^2}$ och g(x) = $\frac{1}{b^2+x^2}$.

Jag gjorde det, men hur går jag tillväga sen?

Du får sätta in vad Fouriertransformerna blir och räkna ut integralen med Fouriertransformerna.

PATENTERAMERA skrev:

Du får sätta in vad Fouriertransformerna blir och räkna ut integralen med Fouriertransformerna.

Jag vet inte hur man gör om jag ska vara ärlig. Dock hittade jag detta för e^-a|x| .

Du räknade ut Fouriertransformen till 1/(a² + x²) i ett annat problem.

Tror det skall bli

$ℱ\left[\frac{1}{a^2+x^2}\right]\left(\omega \right)=\frac{\mathrm{\pi }}{a}{e}^{-a\left|\omega \right|}$,

eller något åt det hållet. Utnyttja det här.

PATENTERAMERA skrev:

Du räknade ut Fouriertransformen till 1/(a² + x²) i ett annat problem.

Tror det skall bli

$ℱ\left[\frac{1}{a^2+x^2}\right]\left(\omega \right)=\frac{\mathrm{\pi }}{a}{e}^{-a\left|\omega \right|}$,

eller något åt det hållet. Utnyttja det här.

Nja jag minns inte att jag gjorde det. Du får länka den tråden isåfall. Men jag minns att jag fick fram fouriertransformen av e^-a|x| till att bli svaret på bilden i #11.

PATENTERAMERA skrev:

Juste men jag förstod aldrig varför mitt svar inte liknar den i #11.  Varför vänder man upp a och pi? Jag vill gärna att det ska stå a/pie^-a|x|. Fouriertransfomerar man a/pie^-a|x| så får man ju a/pi*a/pi*(a^2+w^2)?

$ℱ\left[e^{-a\left|x\right|}\right]\left(\omega \right)=\frac{2a}{a^2+{\omega }^2}$, sedan kan du få ut Fouriertransformen av 1/(a² + x²) genom inverstransformering.

PATENTERAMERA skrev:

$ℱ\left[e^{-a\left|x\right|}\right]\left(\omega \right)=\frac{2a}{a^2+{\omega }^2}$, sedan kan du få ut Fouriertransformen av 1/(a² + x²) genom inverstransformering.

Jag tror tyvärr inte att jag hänger med på fouriertransformen av e^-a|x|. Då stämmer inte mitt svar i #11. Varför är den fel?

Det beror på vilken definition av Fouriertransformen som du använder.

Det vanliga är ${\int }_{-\infty }^{\infty }f\left(x\right)e^{-i\omega x}dx$. Jag tror du delade med 2pi.

Jag använde den vanliga definitionen.

PATENTERAMERA skrev:

Det beror på vilken definition av Fouriertransformen som du använder.

Det vanliga är ${\int }_{-\infty }^{\infty }f\left(x\right)e^{-i\omega x}dx$. Jag tror du delade med 2pi.

Jag använde den vanliga definitionen.

Du ser i #11 vilken jag använde. Det där borde stämma ändå. 

Multiplicera ditt svar med 2pi så får du samma som i #16.

PATENTERAMERA skrev:

Multiplicera ditt svar med 2pi så får du samma som i #16.

Varför ska man göra det? Jag förstår inte riktigt. Jag dubbelkollade med facit precis och mitt svar i #11 stämmer.

Därför att du inte använde den gängse definitionen, utan delade med 2pi.

PATENTERAMERA skrev:

Därför att du inte använde den gängse definitionen, utan delade med 2pi.

Det är den korrekta definitionen jag använde mig av och det står så i kursboken. 

Är du säker? Visa.

PATENTERAMERA skrev:

Är du säker? Visa.

OK. Kör på den definitionen. Då blir transformen av e^-a|x| lika med $\frac{a}{\mathrm{\pi }}·\frac{1}{a^2+{\omega }^2}$.

Vad blir då Fouriertransformen av 1/(a² + x²)?

Det kan vara värt att känna till vissa samband mellan Fouriertransform och dess invers.

Låt $\mathfrak{R}$ vara reverseringsoperatorn definierad genom $\mathfrak{R}\left[f\right]\left(x\right)=f(-x)$.

Då har vi att

${ℱ}^{-1}=2\mathrm{\pi }\mathfrak{R}\mathcal{F}$

$ℱ=\frac{1}{2\mathrm{\pi }}\mathfrak{R}{ℱ}^{-1}$

${\left({ℱ}^{-1}\right)}^2=2\mathrm{\pi }\mathfrak{R}$

${ℱ}^2= \frac{\mathfrak{R}}{2\mathrm{\pi }}$.

PATENTERAMERA skrev:

OK. Kör på den definitionen. Då blir transformen av e^-a|x| lika med $\frac{a}{\mathrm{\pi }}·\frac{1}{a^2+{\omega }^2}$.

Vad blir då Fouriertransformen av 1/(a² + x²)?

Jag tänker mig att det blir e^-a|x| med pi/a faktor för då tar de ut varandra 

$ℱ\left[\frac{a}{\mathrm{\pi }}·\frac{1}{a^2+x^2}\right]\left(\omega \right)=\frac{1}{2\mathrm{\pi }}\mathfrak{R}{ℱ}^{-1}\left[\frac{a}{\mathrm{\pi }}·\frac{1}{a^2+x^2}\right]\left(\omega \right)=\frac{1}{2\mathrm{\pi }}\mathfrak{R}\left[e^{-a\left|\omega \right|}\right]=\frac{1}{2\mathrm{\pi }}{e}^{-a\left|\omega \right|}$.

Vilket implicerar att

$ℱ\left[\frac{1}{a^2+x^2}\right]\left(\omega \right)=\frac{e^{-a\left|\omega \right|}}{2a}$.

PATENTERAMERA skrev:

$ℱ\left[\frac{a}{\mathrm{\pi }}·\frac{1}{a^2+x^2}\right]\left(\omega \right)=\frac{1}{2\mathrm{\pi }}\mathfrak{R}{ℱ}^{-1}\left[\frac{a}{\mathrm{\pi }}·\frac{1}{a^2+x^2}\right]\left(\omega \right)=\frac{1}{2\mathrm{\pi }}\mathfrak{R}\left[e^{-a\left|\omega \right|}\right]=\frac{1}{2\mathrm{\pi }}{e}^{-a\left|\omega \right|}$.

Vilket implicerar att

$ℱ\left[\frac{1}{a^2+x^2}\right]\left(\omega \right)=\frac{e^{-a\left|\omega \right|}}{2a}$.

Jag förstår inte riktigt 

Jag använder bara formlerna i #27 rakt av. Samt att vi vet att

${ℱ}^{-1}\left[\frac{a}{\mathrm{\pi }}·\frac{1}{a^2+x^2}\right]\left(\omega \right)=e^{-a\left|\omega \right|}$.

PATENTERAMERA skrev:

Jag använder bara formlerna i #27 rakt av. Samt att vi vet att

${ℱ}^{-1}\left[\frac{a}{\mathrm{\pi }}·\frac{1}{a^2+x^2}\right]\left(\omega \right)=e^{-a\left|\omega \right|}$.

Vi har inte lärt oss formlerna i #27 men jag håller med om invers transformen av (a/pi*1/(a^2+x^2))

Det finns igen lag som förbjuder att man lär sig något nytt.

Så du är med på att transformen av 1/(a² + x²) blir $\frac{e^{-a\left|\omega \right|}}{2a}$.

Då blir naturligtvis transformen av 1/(b² + x²) på liknande sätt $\frac{e^{-b\left|\omega \right|}}{2b}$.

Nu kan du sätt in det i Plancherels formel och beräkna integralen.

PATENTERAMERA skrev:

Det finns igen lag som förbjuder att man lär sig något nytt.

Så du är med på att transformen av 1/(a² + x²) blir $\frac{e^{-a\left|\omega \right|}}{2a}$.

Då blir naturligtvis transformen av 1/(b² + x²) på liknande sätt $\frac{e^{-b\left|\omega \right|}}{2b}$.

Nu kan du sätt in det i Plancherels formel och beräkna integralen.

Jag är inte med på faktorn 1/2a framför e^-a|w| och vet såklart inte var du får saker ifrån. Jag sa bara att jag är endast med på att invers transformen av a/pi*1/(a^2+w^2)=e^-a|x|

Men hur räknade du ut transformen till 1/(a² + x²) i den andra tråden?

PATENTERAMERA skrev:

Men hur räknade du ut transformen till 1/(a² + x²) i den andra tråden?

Där skrev jag bara F^-1[1/a²+x²]=pi/a*e^-a|x|

Jo men du skulle räkna ut F[1/(a² + x²)](w). Hur gör du det?

PATENTERAMERA skrev:

Jo men du skulle räkna ut F[1/(a² + x²)](w). Hur gör du det?

Ja, det är väl lika med a/pi*e^-a|x|?  Annars vet jag inte hur man enklast får fram den. 

Men hur kom du fram till det, är det något du kan utantill? Eller räknade du ut det med definitionen? Eller hittade du den i en tabell på någon sida i boken?

Du ska alltså räkna ut Fouriertransformen, då vill vi ha en funktion av $\omega$

D4NIEL skrev:

Men hur kom du fram till det, är det något du kan utantill? Eller räknade du ut det med definitionen? Eller hittade du den i en tabell på någon sida i boken?

Det finns ingen tabell i boken om detta. Jag försökte använda definitionen men fastnade redan där och såg att AI fick fram det svaret. Dock vet jag inte på rak arm hur man faktiskt gör mha definitionen. Det såg väldigt svårt ut. 

$$\begin{gathered} e^{-a\left|\omega \right|}={ℱ}^{-1}\left[\frac{a}{\mathrm{\pi }}\frac{1}{a^2+x^2}\right]\left(\omega \right)={\int }_{-\infty }^{\infty }\frac{a}{\mathrm{\pi }}\frac{1}{a^2+x^2}{e}^{i\omega x}dx={\int }_{-\infty }^{\infty }\frac{a}{\mathrm{\pi }}\frac{1}{a^2+x^2}{e}^{-i\left(-\omega \right)x}dx= \\ 2\mathrm{\pi }·\frac{1}{2\mathrm{\pi }}{\int }_{-\infty }^{\infty }\frac{a}{\mathrm{\pi }}\frac{1}{a^2+x^2}{e}^{-i\left(-\omega \right)x}dx=2\mathrm{\pi }\mathcal{F}\left[\frac{a}{\mathrm{\pi }}\frac{1}{a^2+x^2}\right]\left(-\omega \right) \end{gathered}$$

Således får vi

$ℱ\left[\frac{1}{a^2+x^2}\right]\left(\omega \right)=\frac{e^{-a\left|-\omega \right|}}{2a}=\frac{e^{-a\left|\omega \right|}}{2a}$.

PATENTERAMERA skrev:

$$\begin{gathered} e^{-a\left|\omega \right|}={ℱ}^{-1}\left[\frac{a}{\mathrm{\pi }}\frac{1}{a^2+x^2}\right]\left(\omega \right)={\int }_{-\infty }^{\infty }\frac{a}{\mathrm{\pi }}\frac{1}{a^2+x^2}{e}^{i\omega x}dx={\int }_{-\infty }^{\infty }\frac{a}{\mathrm{\pi }}\frac{1}{a^2+x^2}{e}^{-i\left(-\omega \right)x}dx= \\ 2\mathrm{\pi }·\frac{1}{2\mathrm{\pi }}{\int }_{-\infty }^{\infty }\frac{a}{\mathrm{\pi }}\frac{1}{a^2+x^2}{e}^{-i\left(-\omega \right)x}dx=2\mathrm{\pi }\mathcal{F}\left[\frac{a}{\mathrm{\pi }}\frac{1}{a^2+x^2}\right]\left(-\omega \right) \end{gathered}$$

Således får vi

$ℱ\left[\frac{1}{a^2+x^2}\right]\left(\omega \right)=\frac{e^{-a\left|-\omega \right|}}{2a}=\frac{e^{-a\left|\omega \right|}}{2a}$.

Jag hänger inte med tyvärr. Jag hade hoppats att vi går tillbaka till hur vi transformerar 1/(a^2+x^2) mha definitionen.

Jag använde bara definitionen av den inversa transformen, och att vi vet vad den inversa transformen skall bli.

PATENTERAMERA skrev:

Jag använde bara definitionen av den inversa transformen, och att vi vet vad den inversa transformen skall bli.

Jag hänger inte heller med på den biten. Det har blivit mycket rörigare nu. Jag känner mig inte övertygad 

Hänger du med på 1?

PATENTERAMERA skrev:

Hänger du med på 1?

(1) är jag med på för det är sant att inversen av a/pi*1/(a^2+x^2) blir e^-a|w|.  Sen är jag med på 2) , men inte 3)-5)

På 2 utnyttjar vi definitionen av den inversa transformen.

${ℱ}^{-1}\left[F\left(x\right)\right]\left(\omega \right)\equiv {\int }_{-\infty }^{\infty }F\left(x\right)e^{i\omega x }dx$.

PATENTERAMERA skrev:

På 2 utnyttjar vi definitionen av den inversa transformen.

${ℱ}^{-1}\left[F\left(x\right)\right]\left(\omega \right)\equiv {\int }_{-\infty }^{\infty }F\left(x\right)e^{i\omega x }dx$.

Jag är med på 2an. Det handlar mer om 3, 4 och 5. På dessa steg har jag ingen aning om vad som händer och vilka definitioner du utgår ifrån.

Vad vi vill få till är att kunna utnyttja definitionen av Fouriertransformen.

$ℱ\left[F\left(x\right)\right]\left(\omega \right)=\frac{1}{2\mathrm{\pi }}{\int }_{-\infty }^{\infty }F\left(x\right)e^{-i\omega x}dx$.

Det gälller då att

$ℱ\left[F\left(x\right)\right]\left(-\omega \right)=\frac{1}{2\mathrm{\pi }}{\int }_{-\infty }^{\infty }F\left(x\right)e^{-i\left(-\omega \right)x}dx$.

I 3 så skriver vi om iwx till -i(-w)x, det är ju samma sak.

Sedan i 4 så delar jag med 2pi för att det skall stämma med definitionen av Fouriertransformen, men då måste jag ju även multiplicera med 2pi.

Så vi kommer fram till att 

$$\begin{gathered} 2\mathrm{\pi }\mathcal{F} \left[\frac{a}{\mathrm{\pi }}\frac{1}{a^2+x^2}\right]\left(-\omega \right)=e^{-a\left|\omega \right|} \\ 2aℱ\left[\frac{1}{a^2+x^2}\right]\left(-\omega \right)=e^{-a\left|\omega \right|} \\ ℱ\left[\frac{1}{a^2+x^2}\right]\left(\omega \right)=\frac{e^{-a\left|-\omega \right|}}{2a}=\frac{e^{-a\left|\omega \right|}}{2a} \end{gathered}$$

PATENTERAMERA skrev:

Vad vi vill få till är att kunna utnyttja definitionen av Fouriertransformen.

$ℱ\left[F\left(x\right)\right]\left(\omega \right)=\frac{1}{2\mathrm{\pi }}{\int }_{-\infty }^{\infty }F\left(x\right)e^{-i\omega x}dx$.

Det gälller då att

$ℱ\left[F\left(x\right)\right]\left(-\omega \right)=\frac{1}{2\mathrm{\pi }}{\int }_{-\infty }^{\infty }F\left(x\right)e^{-i\left(-\omega \right)x}dx$.

I 3 så skriver vi om iwx till -i(-w)x, det är ju samma sak.

Sedan i 4 så delar jag med 2pi för att det skall stämma med definitionen av Fouriertransformen, men då måste jag ju även multiplicera med 2pi.

Så vi kommer fram till att 

$$\begin{gathered} 2\mathrm{\pi }\mathcal{F} \left[\frac{a}{\mathrm{\pi }}\frac{1}{a^2+x^2}\right]\left(-\omega \right)=e^{-a\left|\omega \right|} \\ 2aℱ\left[\frac{1}{a^2+x^2}\right]\left(-\omega \right)=e^{-a\left|\omega \right|} \\ ℱ\left[\frac{1}{a^2+x^2}\right]\left(\omega \right)=\frac{e^{-a\left|-\omega \right|}}{2a}=\frac{e^{-a\left|\omega \right|}}{2a} \end{gathered}$$

Ok jag är med på allt nu. Frågan är bara hur det blir med absolutbelopptecknet när vi ska integrera sen och hur man gör på det här steget. Se bild nedan.  Det finns ett strecken ovanför som jag inte vet hur man hanterar?

PATENTERAMERA skrev:

Vad vi vill få till är att kunna utnyttja definitionen av Fouriertransformen.

$ℱ\left[F\left(x\right)\right]\left(\omega \right)=\frac{1}{2\mathrm{\pi }}{\int }_{-\infty }^{\infty }F\left(x\right)e^{-i\omega x}dx$.

Det gälller då att

$ℱ\left[F\left(x\right)\right]\left(-\omega \right)=\frac{1}{2\mathrm{\pi }}{\int }_{-\infty }^{\infty }F\left(x\right)e^{-i\left(-\omega \right)x}dx$.

I 3 så skriver vi om iwx till -i(-w)x, det är ju samma sak.

Sedan i 4 så delar jag med 2pi för att det skall stämma med definitionen av Fouriertransformen, men då måste jag ju även multiplicera med 2pi.

Så vi kommer fram till att 

$$\begin{gathered} 2\mathrm{\pi }\mathcal{F} \left[\frac{a}{\mathrm{\pi }}\frac{1}{a^2+x^2}\right]\left(-\omega \right)=e^{-a\left|\omega \right|} \\ 2aℱ\left[\frac{1}{a^2+x^2}\right]\left(-\omega \right)=e^{-a\left|\omega \right|} \\ ℱ\left[\frac{1}{a^2+x^2}\right]\left(\omega \right)=\frac{e^{-a\left|-\omega \right|}}{2a}=\frac{e^{-a\left|\omega \right|}}{2a} \end{gathered}$$

En annan sak som stör mig här är när man skriver e^-a|x| eller e^-a|w|. För jag började med att hitta fouriertransformen till e^-a|x| och ej e^-a|w|. 

destiny99 skrev:

PATENTERAMERA skrev:

Vad vi vill få till är att kunna utnyttja definitionen av Fouriertransformen.

$ℱ\left[F\left(x\right)\right]\left(\omega \right)=\frac{1}{2\mathrm{\pi }}{\int }_{-\infty }^{\infty }F\left(x\right)e^{-i\omega x}dx$.

Det gälller då att

$ℱ\left[F\left(x\right)\right]\left(-\omega \right)=\frac{1}{2\mathrm{\pi }}{\int }_{-\infty }^{\infty }F\left(x\right)e^{-i\left(-\omega \right)x}dx$.

I 3 så skriver vi om iwx till -i(-w)x, det är ju samma sak.

Sedan i 4 så delar jag med 2pi för att det skall stämma med definitionen av Fouriertransformen, men då måste jag ju även multiplicera med 2pi.

Så vi kommer fram till att 

$$\begin{gathered} 2\mathrm{\pi }\mathcal{F} \left[\frac{a}{\mathrm{\pi }}\frac{1}{a^2+x^2}\right]\left(-\omega \right)=e^{-a\left|\omega \right|} \\ 2aℱ\left[\frac{1}{a^2+x^2}\right]\left(-\omega \right)=e^{-a\left|\omega \right|} \\ ℱ\left[\frac{1}{a^2+x^2}\right]\left(\omega \right)=\frac{e^{-a\left|-\omega \right|}}{2a}=\frac{e^{-a\left|\omega \right|}}{2a} \end{gathered}$$

Ok jag är med på allt nu. Frågan är bara hur det blir med absolutbelopptecknet när vi ska integrera sen och hur man gör på det här steget. Se bild nedan.  Det finns ett strecken ovanför som jag inte vet hur man hanterar?

Multiplicera ihop. Eftersom funktionen blir jämn så kan du dubbla integralen från 0 till oändlighet. Strecket betyder komplexkonjugering, men funktionen är reell så du kan skippa strecket.

PATENTERAMERA skrev:

destiny99 skrev:

Visa föregående citat

PATENTERAMERA skrev:

Vad vi vill få till är att kunna utnyttja definitionen av Fouriertransformen.

$ℱ\left[F\left(x\right)\right]\left(\omega \right)=\frac{1}{2\mathrm{\pi }}{\int }_{-\infty }^{\infty }F\left(x\right)e^{-i\omega x}dx$.

Det gälller då att

$ℱ\left[F\left(x\right)\right]\left(-\omega \right)=\frac{1}{2\mathrm{\pi }}{\int }_{-\infty }^{\infty }F\left(x\right)e^{-i\left(-\omega \right)x}dx$.

I 3 så skriver vi om iwx till -i(-w)x, det är ju samma sak.

Sedan i 4 så delar jag med 2pi för att det skall stämma med definitionen av Fouriertransformen, men då måste jag ju även multiplicera med 2pi.

Så vi kommer fram till att 

$$\begin{gathered} 2\mathrm{\pi }\mathcal{F} \left[\frac{a}{\mathrm{\pi }}\frac{1}{a^2+x^2}\right]\left(-\omega \right)=e^{-a\left|\omega \right|} \\ 2aℱ\left[\frac{1}{a^2+x^2}\right]\left(-\omega \right)=e^{-a\left|\omega \right|} \\ ℱ\left[\frac{1}{a^2+x^2}\right]\left(\omega \right)=\frac{e^{-a\left|-\omega \right|}}{2a}=\frac{e^{-a\left|\omega \right|}}{2a} \end{gathered}$$

Ok jag är med på allt nu. Frågan är bara hur det blir med absolutbelopptecknet när vi ska integrera sen och hur man gör på det här steget. Se bild nedan.  Det finns ett strecken ovanför som jag inte vet hur man hanterar?

Multiplicera ihop. Eftersom funktionen blir jämn så kan du dubbla integralen från 0 till oändlighet. Strecket betyder komplexkonjugering, men funktionen är reell så du kan skippa strecket.

Detta är vad jag kom fram till. Dock håller inte facit med och de har en faktor 2pi utanför integralen som jag inte förstår varifrån de får detta ifrån. 

2pi kommer från Plancherels formel i #7.

Sedan har du gjort fel på primitiva funktionen. Teckenfel.

PATENTERAMERA skrev:

2pi kommer från Plancherels formel i #7.

Sedan har du gjort fel på primitiva funktionen. Teckenfel.

Men i #7 har de 1/2pi innan man tar fouriertransform på f(x). Jag ser inte vilket fel jag gjort på primitiva funktionen. 

PATENTERAMERA skrev:

Jag förstår inte din lösning.

Var tappar du bort dig?

PATENTERAMERA skrev:

Var tappar du bort dig?

Början till slut. Har svårt att följa din lösning. 

Vi börjar med den integral som vi skall lösa. Den går från noll till oändlighet.

Sedan ser vi att den är halva integralen från -oändlighet till oändlighet. Pga jämn integrand.

Efter det så utnyttjar vi Plancherels formel för att skriva om integralen som en integral över Fouriertransformerna i stället. 2pi kommer från Plancherels formel.

Jämn funktion så vi kan multiplicera med 2 och integrera från 0 till oändlighet. Klart.

PATENTERAMERA skrev:

Vi börjar med den integral som vi skall lösa. Den går från noll till oändlighet.

Sedan ser vi att den är halva integralen från -oändlighet till oändlighet. Pga jämn integrand.

Efter det så utnyttjar vi Plancherels formel för att skriva om integralen som en integral över Fouriertransformerna i stället. 2pi kommer från Plancherels formel.

Jämn funktion så vi kan multiplicera med 2 och integrera från 0 till oändlighet. Klart.

Så när jag ska integrera #53 så ska jag 2pi i första raden?

Plancherels säger - se #7.

${\int }_{-\infty }^{\infty }f\left(x\right)\overline{g\left(x\right)}dx=2\mathrm{\pi }{\int }_{-\infty }^{\infty }\mathrm{F}\left(\mathrm{\omega }\right)\overline{\mathrm{G}\left(\mathrm{\omega }\right)}\mathrm{d\omega }$. Där kommer 2pi in.

PATENTERAMERA skrev:

Plancherels säger - se #7.

${\int }_{-\infty }^{\infty }f\left(x\right)\overline{g\left(x\right)}dx=2\mathrm{\pi }{\int }_{-\infty }^{\infty }\mathrm{F}\left(\mathrm{\omega }\right)\overline{\mathrm{G}\left(\mathrm{\omega }\right)}\mathrm{d\omega }$. Där kommer 2pi in.

Ok. Man ska alltså multiplicera upp till 2pi till högerledet så det stämmer med formeln på vänsterledet. 

Ja.