Tillägg av pi

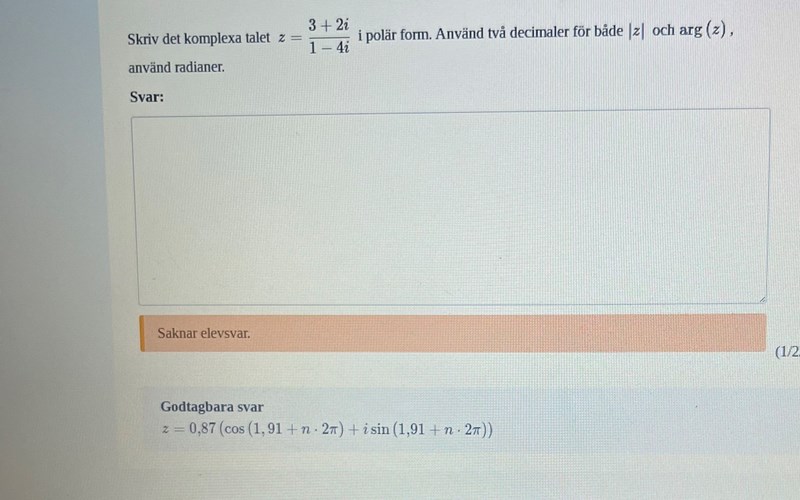
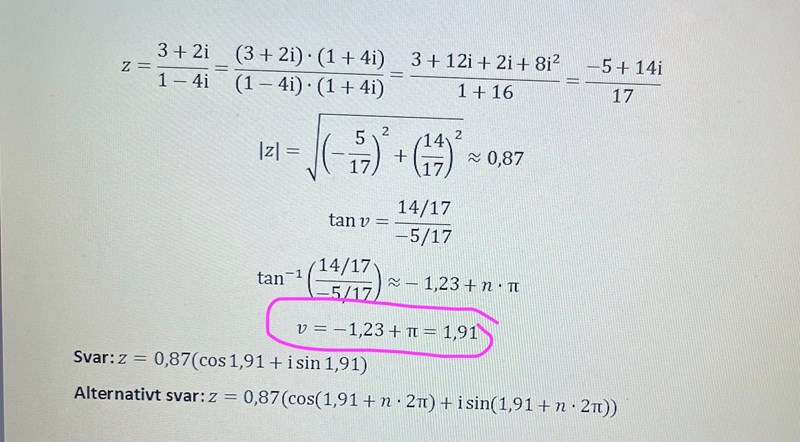
Man kan ju beräkna argumentet av ett komplext tal $z$ genom förhållandet

$\displaystyle \tan v = \frac ba$

där $v = \arg z$ och $z = a+bi$.

Alltså att tan av arguumentet är kvoten mellan imaginär och realdelen. 

Då kan man tänka sig att

$\displaystyle v = \tan^{-1}\left(\frac ba\right)$              (1)

Men det finns ett problem med detta. 

Om vi kollar på de två komplexa talen $z = 1+ i$ och $w = -1 -i$. 

Man kan få fram att $\arg z = \frac \pi 4$ och $\arg w = \frac{5\pi}4$. 

Om man använder formeln (1) får man att 

$\displaystyle \arg z = \tan^{-1}\left(\frac 11\right) = \tan^{-1} \left(1\right) = \frac \pi 4$

Inga konstigheter här, men för $w$:

$\displaystyle \arg w = \tan^{-1}\left(\frac {-1}{-1}\right) = \tan^{-1}\left(1\right) = \frac \pi 4$

Vilket inte stämmer. 

Formeln $\tan v = \frac ba$ kommer ifrån att dela upp rörelse i reell led och imaginärled.

Om $\tan v$ är positiv kan det komplexa talet antingen vara i den tredje eller första kvadranten. Då är kvoten mellan real och imaginärdel positiv. 

Om $\tan v$ är negativ kan det komplexa talet antingen vara i den andra eller fjärde kvadranten. 

De två möjliga talen kommer alltid skilja sig med ett argument av $\pi$. Då är det bara att inspektera talet och se vilken kvadrant den ligger i för att förstå om man behöver addera $\pi$ eller inte!