Tillämpning av extremvärden till Koordinatgeometri

Frågan: En linje genom punkten (2, 5) bildar tillsammans med koordinataxlarna i första kvadranten en triangel. Bestäm linjens ekvation så att triangelns area blir så liten som möjligt.

Jag tror att jag ska komma på en funktion som typ beskriver arean på triangel beroende på vad för k och m värden linjens ekvation har. Sen antar jag att jag ska hitta minimum-värdet på funktionen.?

Problemet är att jag vet inte hur jag ska skriva den här funktionen, jag vet bara att k-värdet måste vara negativ för annars blir det ingen triangel.

För att kunna skriva en funktion för arean behövs höjd och bredd på triangeln. Eftersom den börjar i "origohörnet" är det samma som x och y där linjen skär axlarna. Kan du lösa ut någon av dem från k-värdet? Jag brukar tänka på det som k=(rutor upp) /(rutor fram).

(kx+m) m är vart linjen skär y-axeln så höjden är m?

Om du ändrar på m, hur ändrar sig skärningen med x-axeln? Prova rita upp några exempel och se om du kan få fram en formel från det.

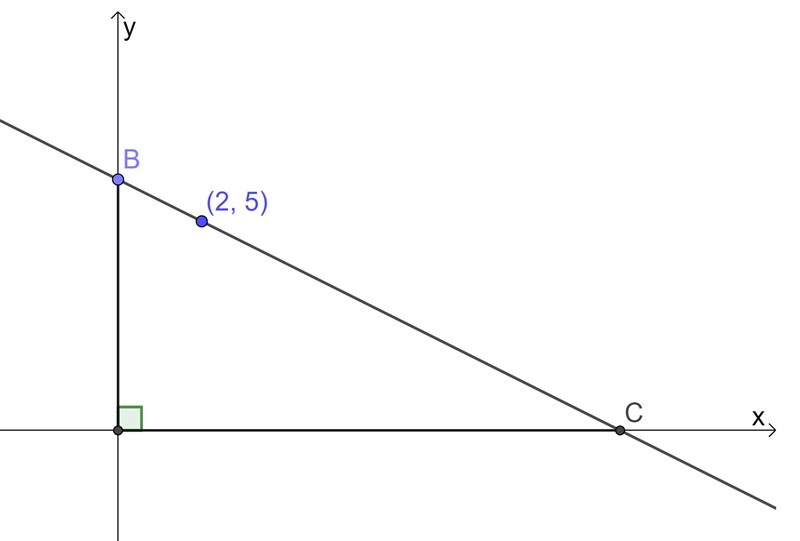
Bestäm uttryck för B och C:

$f (x) = k x + m f (2) = 5 5 = 2 k + m m = 5 - 2 k P u n k t e n B : (0, m) = (0, 5 - 2 k) ⋮ f (x) = k x + m m = 5 - 2 k f (x) = k x + (5 - 2 k) s k ä r n i n g m e d x - a x e l : f (x) = 0 0 = k x_{0} + (5 - 2 k) \frac{2 k - 5}{k} = x_{0} P u n k t e n B : (x_{0}, 0) = (\frac{2 k - 5}{k}, 0) ⋮ A r e a t r i a n g e l = \frac{b h}{2} = \frac{(\frac{2 k - 5}{k}) (5 - 2 k)}{2} = \frac{(2 k - 5) (5 - 2 k)}{2 k} = - \frac{(5 - 2 k) (5 - 2 k)}{2 k} = - \frac{{(5 - 2 k)}^{2}}{2 k} A (k) = - \frac{{(5 - 2 k)}^{2}}{2 k}$

När antar A(k) sitt minsta värde?

Uhm... Det måste vara nära 2.5?

0 är onekligen en liten area, men det fallet uppstår när både B och C är origo, och det var nog inte vad de tänkte sig, fast det inte förbjuds uttryckligen,

Är ni säkra att funktionen är rätt..?

Har du provat att hitta alla extrempunkter till den?

jag hittade bara 2.5

Vad är A'(k)?

SuchdaKawaii skrev:
jag hittade bara 2.5

k ska inte vara positivt. du sa ju själv att det inte blir en triangel då...

oop menade -2.5

Du måste ha hittat både -2,5 och 2,5.

Ja och i så fall -2.5 är lämplig. Blir inte m-värdet då uppenbart?

$A (k) = - \frac{{(5 - 2 k)}^{2}}{2 k} = {- \frac{1}{2} (5 - 2 k)}^{2} k^{- 1} A' = (- (5 - 2 k) * - 2) k^{- 1} {- \frac{1}{2} (5 - 2 k)}^{2} * - k^{- 2} = \frac{2 (5 - 2 k)}{k} + \frac{{(5 - 2 k)}^{2}}{2 k^{2}} = \frac{2 (5 - 2 k) * 2 k}{k * 2 k} + \frac{{(5 - 2 k)}^{2}}{2 k^{2}} = \frac{4 k (5 - 2 k) + {(5 - 2 k)}^{2}}{2 k^{2}} = \frac{20 k - 8 k^{2} + {(5 - 2 k)}^{2}}{2 k^{2}} A' = 0 20 k - 8 k^{2} + {(5 - 2 k)}^{2} = 0 20 k - 8 k^{2} + {(5 - 2 k)}^{2} = 20 k - 8 k^{2} + 25 - 20 k + 4 k^{2} = - 4 k^{2} + 25 - 4 k^{2} + 25 = 0 k = \pm 2.5$

y=kx+m
y=-2.5x+m
m=5-2k=5-2*-2.5=10

Svar:

y=-2.5x+10

Jag skulle vilja påstå att det här är en A-uppgift. Man behöver inte använda produktregeln vid deriveringen. Istället kan man expandera och dela upp $A (k) = - \frac{{(5 - 2 k)}^{2}}{2 k}$ .

Kommer såna hära svåra frågor finnas I NP for Matematik 3C? I så fall är jag rökt

Man man kan väll få hyffsat på NP även om man inte kan A-uppgifterna.

Svara

Visa senaste svar