Tillhör en vektor Col(A)? Linjär Algebra
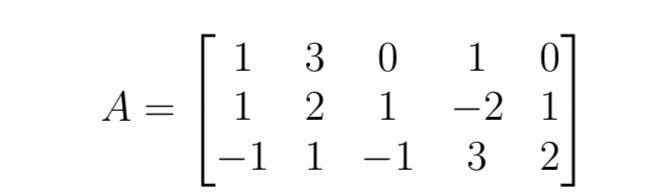

För att se om b tillhör Col(A) ställer man upp ekvationen Ax=b. Jag har gjort det och kom fram till att lösningsmängden är (x1 ,x2 , x3 , x4 , x5)= (-1, (2/3), (2/3), 0,0) + s(0,(-1/3), (8/3), 1,0)+ t(3,-1,-2,0,1). Betyder detta att b tillhör ColA då jag systemet inte är inkosistent? Jag vet inte riktigt hur jag ska tolka det jag kom fram till.
Hej,
Det finns en sats eller regel som säger att en vektor tillhör ett span (dvs. Col(A)) om och endast om det kan skrivas som en linjär kombination av vektorerna i spannet, dvs. om det finns minst en lösning till Ax=b (x och b är vektorer, hittar inte dom där strecken dom ska ha ovanpå).
Eftersom du tagit fram en lösningsmängd där jag antar s och t kan anta alla reella värden har du definitivt minst en lösning.
Okej tack!
Så lite så :)
I en annan tråd visade du att de tre första kolonnerna av utgör en bas för värderummet (kolonnrummet). Basen spänner hela . Det innebär att varje vektor också tillhör . I just det här fallet visar det sig att:
Där är de tre första kolonnerna i . Vektorn är uppenbarligen en linjärkombination av det tre första kolonnerna.
Lösningsmängden är korrekt uträknad och det kan vara värt att notera att vektorerna framför parametrarna och är de vektorer som spänner nollrummet till .
Dvs alla lösningar till kan ses som summan av någon vektor från nollrummet som löser den homogena ekvationen och någon partikulärlösning . Ty
Man säger att lösningsmängden till kan skrivas som där är nollrummet till . Lösningsmängden är alltså en affin mängd.
Tack så mycket!!


