tolka lösningen av en olikhet

jag har lite problem med att tolka lösningen jag kommer fram till i följande olikhet:

$|x - 2| < \sqrt{2 x + 4} a l t e r n a t i v I : x - 2 < \sqrt{2 x + 4} x^{2} - 4 x + 4 < 2 x + 4 x^{2} - 6 x < 0 x (x - 6) < 0 x_{1} < 0 x_{2} < 6 a l t e r n a t i v I I : - x + 2 < \sqrt{2 x + 4} x^{2} + 4 x + 4 < 2 x + 4 x^{2} + 2 x < 0 x (x + 2) < 0 x_{3} < 0 x_{4} < - 2$

när jag försöker tolka de här resultaten fastnar jag.

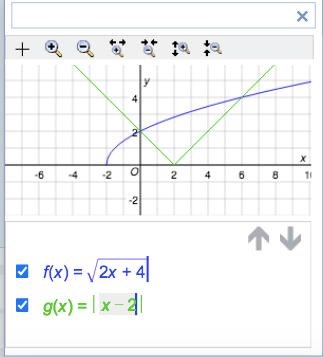
när jag istället löser olikheten grafiskt kan jag se vad alla x-värden faktiskt betyder: -2 är början på den blå grafen, 0 är vänstra punkten där graferna möts och 6 är den högra. så svaret på olikheten ska ju bli 0<x<6. men detta förstår jag först när jag tittar på den grafiska lösningen. när jag bara ser det algebraiskt förstår jag inte.

varför får jag x<0 algebraiskt när det grafiskt blir x>0? och varför jag får fram x-värdet -2 när jag jämför de båda graferna– det värdet är ju bara relevant för den ena grafen?

hur ska jag tänka för att kunna tolka min algebraiska lösning på rätt sätt, och enbart därigenom komma fram till svaret på olikheten?

Uttryckt under rotmärket får inte bli negativt.

För vilka värden på x gäller alternativ I? För vilka värden på x gäller alternativ II?

Alternativ 2: Om VL skall vara negativt så krävs det att x och (x+2) har olika tecken. För vilka värden på x är detta sant?

$a l t I g ä l l e r o m x - 2 \geq 0 x \geq 2 a l t I I g ä l l e r o m x - 2 < 0 x < 2$

$o m x (x + 2) < 0 m å s t e x < - 2$

jag förstår inte hur detta hjälper :(

Fall 1 gäller om x>2 Vilka av lösningarna x<0 och x<6 funkar?

Fall 2 gäller om x<2. Vilka av lösningarna stämmer då? (Fast jag förstår inte hur du fick fram de båda lösningarna - det verkar som om du glömmer att vända på olikhetstecknet när du multiplicerar med ett negativt tal, åtminstone ibland.

Smaragdalena skrev:
Fall 1 gäller om x>2 Vilka av lösningarna x<0 och x<6 funkar?
Fall 2 gäller om x<2. Vilka av lösningarna stämmer då? (Fast jag förstår inte hur du fick fram de båda lösningarna - det verkar som om du glömmer att vända på olikhetstecknet när du multiplicerar med ett negativt tal, åtminstone ibland.

har jag fattat det rätt?

1. lös olikheten mellan de båda graferna för alternativ I (positivt) och II (negativt)
2. ta reda på hur stort värdet på x kan vara i alternativ I respektive II
3. svaret hamnar mellan de x-värden som stämmer överens med informationen i steg 2

Hej Alm,

Kvadreras olkheten $0\leq |x-2| < \sqrt{2x+4}$ får man -- på grund av att funktionen $f(x) = x^2$ är strängt växande på intervallet $[0,\infty)$

$0 \leq (x-2)^2 < 2x+4\iff 0 \leq x^2-4x+4<2x+4\iff-2x-4 \leq x^2-6x<0.$

Olikheten $x^2-6x < 0$ är uppfylld endast om $0<x<6.$
Olikheten $-2x-4 \leq x^2-6x \iff 0 \leq x^2 - 4x + 4 \iff 0 \leq (x-2)^2$ är uppfylld av alla reella $x.$

Svara Avbryt

Visa senaste svar