Torque
Hej,
Jag fick en hel del förklaring om mass centrum och moment arm men jag är ff hemsk förvirrad.
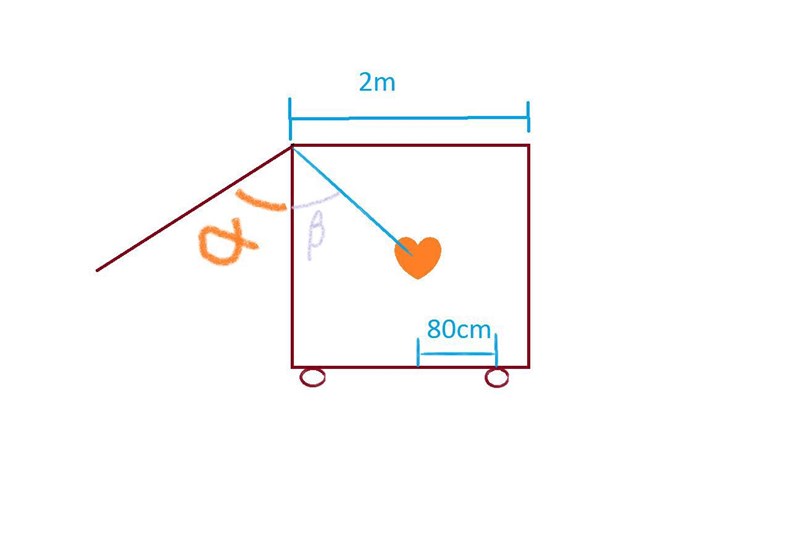
Jag måste räkna ut vridmoment för en låda. Jag har gjort en lite schema för uppgiften, oranga hjärtat är masscentrumet.
Måste jag jämföra, på höger sidan Mg som vill rotera medurs, och på vänster sidan cos alpha * 1m *mg? Eller är det sqrt(8)/2 som är moment arm och vinkel alpha+ beta?
Alltså mg*0.8=1*cos alpha*N?
Eller mg*0.8 = sqrt(8)/2*cos (alpha+beta)*N??
Det känns logisk att moment armen är från kanten till centrum men eftersom vektorer kan flyttas på deras verkningsaxeln... Jag vet absolut inte hur jag måste angripa saken.
Det skulle underlätta om man fick läsa originaltexten till denna uppgift.
Lådans vikt tycks vila på de två hjulen.
Välter man sedan lådan med vinkel alfa eller...?
Yep det vältar med vinkel alpha...
Det är en inlämningsuppgift så jag måste nog lösa den själv. Men principmässigt, kan förklara momentarmen?
Låt oss säga att du välter runt det vänstra hjulet.
Vid en viss vinkel alfa pekar g-vektorn från hjärtat och rakt genom det vänstra hjulet
Rita då en sådan figur.
Rita en linje från hjärtat till precis mellan hjulen
Vinkeln mellan dessa två linjer är tippvinkeln alfa.
Tack så mycket!
Jag ritar och återkommer :)
Affe Jkpg skrev :Låt oss säga att du välter runt det vänstra hjulet.
Vid en viss vinkel alfa pekar g-vektorn från hjärtat och rakt genom det vänstra hjulet
Rita då en sådan figur.
Rita en linje från hjärtat till precis mellan hjulen
Vinkeln mellan dessa två linjer är tippvinkeln alfa.
Hej,
Förlåt för sent svar!
Du menar så? (vinkel beta mellan en rakt linje som går igenom dom 2 stödben och vänsta ben)?
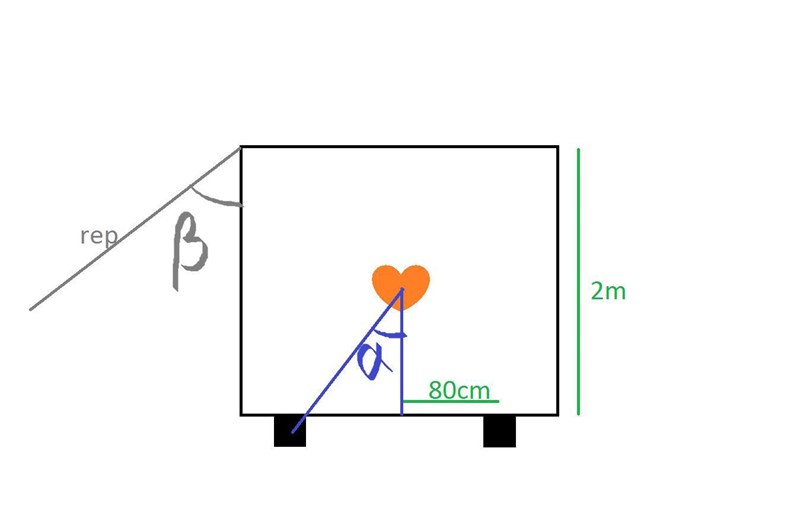
Sorry min fd post var inte så tydligt: det är inte hjul utan små stöd. Och man drar möbeln med en rep som bygger vinkel alpha.
Och varför 0.8 mg = (0.8+0.8+0.2)* F? (vänster led förstår jag)
Daja skrev :Affe Jkpg skrev :Låt oss säga att du välter runt det vänstra hjulet.
Vid en viss vinkel alfa pekar g-vektorn från hjärtat och rakt genom det vänstra hjulet
Rita då en sådan figur.
Rita en linje från hjärtat till precis mellan hjulen
Vinkeln mellan dessa två linjer är tippvinkeln alfa.
Hej,
Förlåt för sent svar!
Du menar så? (vinkel beta mellan en rakt linje som går igenom dom 2 stödben och vänsta ben)?
Sorry min fd post var inte så tydligt: det är inte hjul utan små stöd. Och man drar möbeln med en rep som bygger vinkel alpha.
Och varför 0.8 mg = (0.8+0.8+0.2)* F? (vänster led förstår jag)
Som sagt....Det skulle underlättat om man fått läsa originaltexten eller något liknande till denna uppgift.
Jag antog att du skulle beskriva hur man tippade lådan genom att lyfta med kraften F i nedre högra hörnet.
Nu ska vi i stället dra med ett rep i övre vänstra hörnet
Om beta är 90 grader får du i början av draget:
0.8mg=2*F
Sedan får du komplettera ovanstående när beta inte är 90 grader
Lådan välter fortfarande vid vinklar alfa >38.7 grader. Rita gärna en sådan låda
Vi bortser från stödbenens höjd.
Egentligen går det inte bortse från stödbenens höjd.
Beroende på hur höga dom är så välter lådan antingen runt vänster ben eller runt vänster hörn.
När lådan börjat tippa beror kraften i repet både på vinkeln beta och tippvinkeln. Den momentekvationen tycks lite väl komplicerad för denna uppgift.
Vi har fortfarande inte fått veta vad uppgiften är.
Hej, som sagt det är en inlämningsuppgift så jag vill inte ha svar (och jag vill inte posta frågan) utan förstå principen.
Jag försöker att posta nåt tydligare så fort jag hinner. Tack för allt hjälp!
Hej igen!
Jag har kollat igen: i uppgiften finns det ingenting om föttarna höjden, bara att dom är små, och deras avstånd från kanten!
Frågan 1.är, vad om vinkel som byggs av reppen är 90 grader? Jag har en koef μ for friktion och en tyngd så jag kan räkna ut när det kommer att börja glida. Fråga 2. är, när möbel kommer att välta om vinkel är nu 0 grader (alltså om man drar rakt ner)? Och sista fråga är att beskriva vad händer med möbeln (glida eller välta) som en funktion av vinkeln.
Igen, sorry för otydlighet, men det är en inlämningsfråga. Så det är ok att få hjälp men inte att få det löst, såklart!
Och jag vet inte hur jag ska räkna ut när möbeln vältar (eller vad är momentarm här). Jag har också ingen aning om hur man skriver det som en funktion av vinkeln.
Jag är verkligen jättetacksam för hjälpen. Om ni tycker att det går inte att förklara med så lite information ska jag försöka själv igen :)
När möbeln välter finns det en punkt som den vrider sig runt, momentpunkten. Vilken är den punkten?
Vridmoment är kraft gånger hävarm. Det kan vara lite knepigt att "se" hävarmen ibland, men gör så här: Rita ut kraftens riktning som en lång linje (åt bägge håll, både i kraftens riktning och åt andra hållet). Då blir det lättare att hitta minsta avståndet från den linjen till momentpunkten. Ser du att det avståndet är vinkelrätt mot kraftens riktningslinje? Det avståndet är hävarmen.
Nu tror jag att du hittar alla krafter, och deras hävarm runt momentpunkten.
EDIT: Gjorde ett par snabba redigeringar för tydlighets skull.
Bubo skrev :När möbeln välter finns det en punkt som den vrider sig runt, momentpunkten. Vilken är den punkten?
Vridmoment är kraft gånger hävarm. Det kan vara lite knepigt att "se" hävarmen ibland, men gör så här: Rita ut kraftens riktning som en lång linje (åt bägge håll, både i kraftens riktning och åt andra hållet). Då blir det lättare att hitta minsta avståndet från den linjen till momentpunkten. Ser du att det avståndet är vinkelrätt mot kraftens riktningslinje? Det avståndet är hävarmen.
Nu tror jag att du hittar alla krafter, och deras hävarm runt momentpunkten.
EDIT: Gjorde ett par snabba redigeringar för tydlighets skull.
Jo, det är verkligen knepigt!
Menar du såhär?
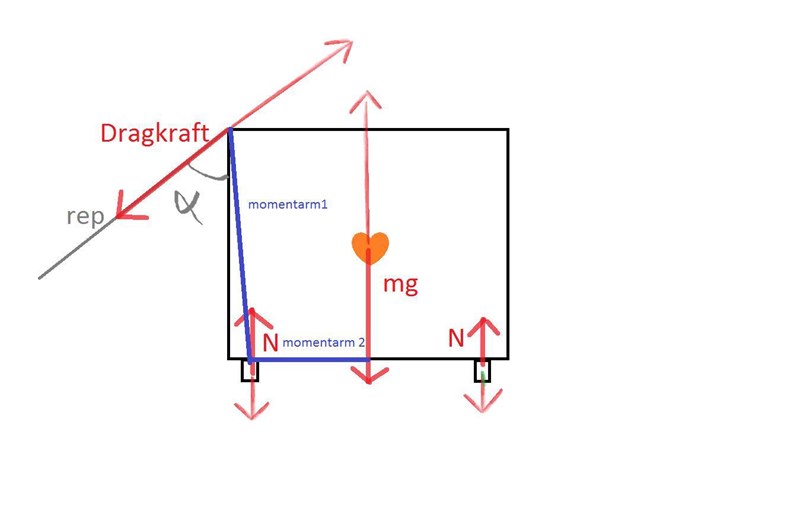
Jag har ritat krafterna åt både riktning och försökt hitta den kortaste avstånd till vridpunkten. Momentarm 1 blev inte vinkelrätt eftersom vinkeln varierar. Jag hoppas att jag har fattat den här gången!
Börja med att rita dom enkla figurerna först!
Sedan kan du komplettera och gör det mer komplicerat.
Börja därför med att rita när alfa=90 grader och "momentarm 1" är vinkelrät.
Tänka på att du har fyra "N"-pilar fast du i figuren korrekt kan rita två.
Rita även kraftpilar riktade åt höger, vinkelräta med dina "N"-pilar. Dessa är friktionskrafterna.
Så länge som lådan glider har du inga momentkrafter.
Skriv kraft-ekvationen för detta fall.
När friktionskrafterna är större än kraften i repet, stannar lådan, det högra benparet börjar lyftas och det uppstår momentkrafter.
Skriv momentekvationen för detta första enklaste fall.
Komplettera sedan momentekvationen med att vinkeln alfa inte är 90 grader
osv.
Tack för hjälpen. Jag hatar den här dumma låda...
Så om vi säger att den har tyngd 1000N och friktion koef. 0.3 då har vi=
F=mg*0.3=300N, så friktion kompenserar upp till 300N och lådan börjar glida.
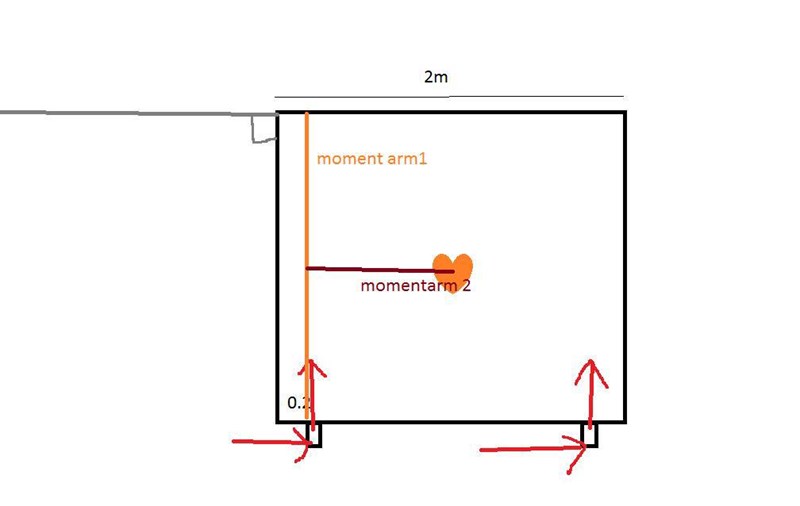
Moment uppstår när mg*0.8=F*1.8
800/1.8=444N, är det så där det funkar?
Jag måste väl multiplicera med cos 90 nångång, eftersom sista fråga är att skriva allt som en funktion av vinkeln... men cos90=0?
Om nu vinkeln = 0grader vet jag inte ens hur jag måste börja med momentarm...
Daja skrev :Tack för hjälpen. Jag hatar den här dumma låda...
Så om vi säger att den har tyngd 1000N och friktion koef. 0.3 då har vi=
F=mg*0.3=300N, så friktion kompenserar upp till 300N och lådan börjar glida.
Moment uppstår när mg*0.8=F*1.8
800/1.8=444N, är det så där det funkar?
Jag måste väl multiplicera med cos 90 nångång, eftersom sista fråga är att skriva allt som en funktion av vinkeln... men cos90=0?
Om nu vinkeln = 0grader vet jag inte ens hur jag måste börja med momentarm...
Nu börjar din låda snart beskriva en verklighet!
Rita som tidigare en pil "mg" rakt ner från "hjärtat".
Skriv där du markerat vinkeln.
Du har fyra fötter på lådan. På varje fot vilar då 250N.
När lådan glider ska repet dra, för att fyra fötter bromsar med:
F=0.3*4*250N
Så där hade du rätt!
men...
1000*0.8=F*2.0
Hej igen!
Vilket fruktansvärt frustrerande uppgift :'/
Friktion motverkar den horisontalla komponent av F, och lådan börjar glida när friktionen är fullt utbildad. Så länge F*sin alpha < friktion lådan glider inte...
Så för att räkna friktion:
4*(mg/4)*0.3 (mu koef)= 300 N
Om vinkel är nu rakt ner, det är i jämvikt så länge mg*det ljusgröna avståndet =F*det röda avståndet (från kanten till fotten)
1000*0.8=F*0.2 eller? Så F måste vara stor isf, =4000 N?
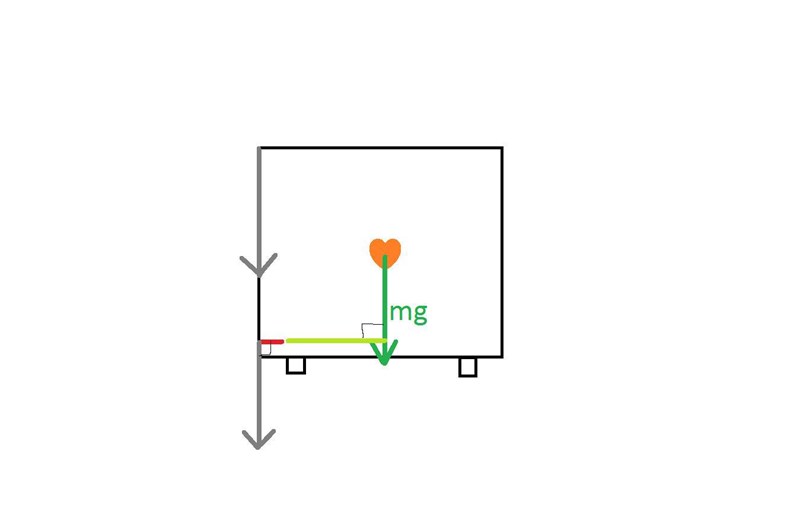
Så för att räkna när det välter respektiv glider räknar vi kvotten av den vertikala vs den horisontella komponent?
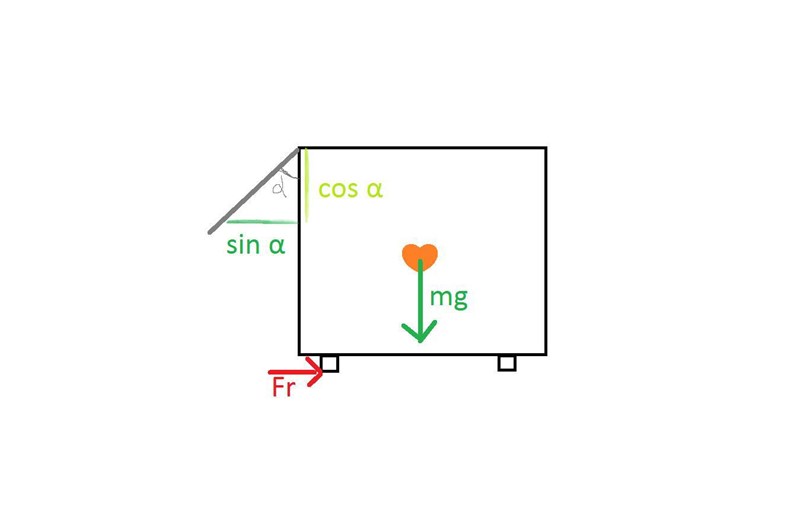
När den vertikala komponent är större en friktiokraften då börjar lådan att välta?
F*sin alpha < F*μ*cos alpha
F*(sin alpha/cos alpha)< F*(cos alpha/cos alpha)*0.3
Tan<0.3? Så när alpha är mindre än 17 grader välter lådan och över 17 grader den glider eftersom den horisontella komponent är nu större än den vertikala??
Förlåt för antalet frågatecken men jag är totalt osäker av vad jag skriver. Förlåt för svenskan också,för trött för att tänka ordentligt på ordföljd och grammatik!
Ta det lugnt, det är inte så noga med ordföljd och grammatik!
4000N är korrekt!
Du tycks vara nära en slutgiltig lösning men...
Affe Jkpg skrev :Ta det lugnt, det är inte så noga med ordföljd och grammatik!
4000N är korrekt!Du tycks vara nära en slutgiltig lösning men...
Hej igen :)
Nu har jag funderat en hel del på det igen... men varför +mg? Kan du snälla förklara lite till?
Är det inte att om friktionen är fullt utbildad och vinkel har rätt storlek valtar boxen, om friktion inte är fullutbildad, glider den?
Jag driver inte med dig, jag verkligen hänger inte med :''(.
Daja skrev :Affe Jkpg skrev :Ta det lugnt, det är inte så noga med ordföljd och grammatik!
4000N är korrekt!Du tycks vara nära en slutgiltig lösning men...
Hej igen :)
Nu har jag funderat en hel del på det igen... men varför +mg? Kan du snälla förklara lite till?
Är det inte att om friktionen är fullt utbildad och vinkel har rätt storlek valtar boxen, om friktion inte är fullutbildad, glider den?
Jag driver inte med dig, jag verkligen hänger inte med :''(.
"F*cos(α)" ger både ett vridmoment på lådan samt ökar kraften på fötterna
Friktions-ekvation:
Moment-ekvation:
Affe Jkpg skrev :Daja skrev :Affe Jkpg skrev :Ta det lugnt, det är inte så noga med ordföljd och grammatik!
4000N är korrekt!Du tycks vara nära en slutgiltig lösning men...
Hej igen :)
Nu har jag funderat en hel del på det igen... men varför +mg? Kan du snälla förklara lite till?
Är det inte att om friktionen är fullt utbildad och vinkel har rätt storlek valtar boxen, om friktion inte är fullutbildad, glider den?
Jag driver inte med dig, jag verkligen hänger inte med :''(.
"F*cos(α)" ger både ett vridmoment på lådan samt ökar kraften på fötterna
Friktions-ekvation:
Moment-ekvation:
Pfff nu har jag suttit en fruktansvärt lång tid igen på den...
I friktion ekvationen tar vi alla vertikala krafter (F cos alpha + mg) gånger mu, och sätter dom lika med den horisontella komponent. F*sin alpha.
I moment ekvationen, varför räknar vi inte normala kraften från den andra foten? Alltså:
N från fotten 2 (den åt höger!)* 1.8 + höjden * F sin alpha + 0.2* F cos alpha = mg*0.8?
Moment-ekvationen beräknas runt den punkt där vänstra foten möter golvet, eftersom lådan har vridnings-centrum runt denna fot. Låda vrider sig alltså runt denna punkt. Fothöjden skulle vi anta vara noll. Momentarmen för "" är då 2m lång
Friktions-ekvationen räknas på alla fyra fötterna samtidigt!
...eller om man ska vara noggrann...
I verkligheten vrider sig lådan runt de två vänstra fötterna och glider på alla fyra.
I din bild (och i ekvationerna) har vi förenklat det:
Lådan vrider sig runt den vänstra foten och glider på en enda fot (gemensam för alla fyra).
Tack för allt! Jag borde verkligen lämna in uppgiften nu:)
Lådan tycks börja tippa (de två högra fötterna lyfter) när:
Så man kan roa sig med att räkna ut:
Ekvationen för när lådan välter, utan att man drar i snöret, är en helt annan :-)
Affe Jkpg skrev :Lådan tycks börja tippa (de två högra fötterna lyfter) när:
Ff≥Fm
Så man kan roa sig med att räkna ut:
Ff=Fm
Ekvationen för när lådan välter, utan att man drar i snöret, är en helt annan :-)
Haha den tror jag har jag räkna ut av misstag. Funkar det med Pythagoras sats?
Förlåt,jag menade, kan vi räkna x och y komponenter med Pythagoras sats och på så sätt räkna ut vinkeln vi letar efter som en tangent?
Vi får anta tillräckligt höga ben, så att lådan hela tiden vrider sig runt vänster ben i din figur och inte börjar vrida sig runt vänster hörn.
Lådan välter då av sig själv när lådan tippar vinkeln :
Rita gärna när detta inträffar och förklara varför lådan då välter :-)
Ok, jag lovar att göra det så fort jag hinner. Har massor uppgifter som dyker upp en efter den andra just nu :/
Nu har jag äntligen löst den ursprungliga problem, så jag tror jag vet hur man gör!
Vi skriver vältningen och glidningen som en funktion av vinkeln, och vi ser grafisk att över 38.7 lådan kommer alltid att glida först, och över 38.7 kommer den alltid att välta först, för det kräver mindre kraft.
Är det det .)?
Nähädu...nu luras du!
Du tycks inte ha ritat lådan när den lutar 38.7 grader!
Rita lådan och rita i vilken riktning vektorn "mg" pekar.
Beskriv varför lådan välter av sig själv, när vinkeln är större än 38.7 grader, oavsett om lådan glider eller inte.
Ahh men just det, om vinkel är större än 38.7 mg pekar över benet, som är stödet, eller hur?
...nu blev jag imponerad!
Affe Jkpg skrev :...nu blev jag imponerad!
What? På riktigt?
Haha nu blev jag glad :)



