Transformation till sfäriska koordinater
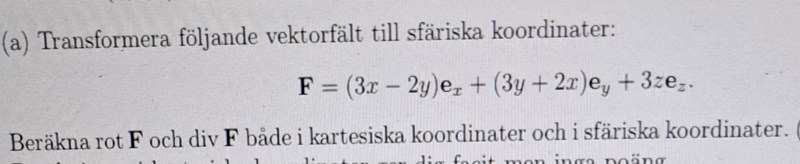

Hej!
När jag stoppade in följande basvektorer och transformationsekvationer i vektorfältet så undrar jag om jag ska göra någon skalärprodukt mellan termerna och deras basvektorer uttryckta i sfäriska koordinater? Till exempel har första termen ingen z-komponent. Efter lite förenkling kommer jag fram till detta längst ned.

Jag ska tydligen använda mig av denna formel från formelsamling för div A samt rotA , men jag vet inte hur jag ska lägga in detta tillsammans med min förenklade term på slutet. Sen förstår jag inte vad de här h1,h2,h3 står för.

F är ju en vektor, men vad du fram på sista raden är en skalär. Tänk på vad som kan gått fel.
h-värdena står längst ner under ”specialfall”.
Notera också att vektorfältet är uttryckt i basvektorer , och i uppgiftens frågeställning.
Du har dock stoppat in , och , d.v.s. en annan uppsättning av basvektorer, d.v.s. en fel bas.
LuMa07 skrev:Notera också att vektorfältet är uttryckt i basvektorer , och i uppgiftens frågeställning.
Du har dock stoppat in , och , d.v.s. en annan uppsättning av basvektorer, d.v.s. en fel bas.
Nu har jag gjort på det sättet istället. Jag hoppas det blev bättre. Men är det inte dessa basvektorer vi ska använda oss av? Efter lite förnekling får jag 3R för Fr komponenten.

PATENTERAMERA skrev:F är ju en vektor, men vad du fram på sista raden är en skalär. Tänk på vad som kan gått fel.
h-värdena står längst ner under ”specialfall”.
Jaha ok. Och A1 är den nya komponenten uttryckt i sfäriska basen och u1, u2 och u3 är alltså (x,y,z) uttryckt i sfäriska koordinater dvs (r,theta,phi)?
Det är korrekt att blir , jättebra! Men hur blir det med ?
Nu har du ju redan räknat ut men det kan vara bra att se att det finns en genväg också. Man kan nämligen skriva fältet så här
Och där kanske man till exempel känner igen och
D4NIEL skrev:Det är korrekt att blir , jättebra! Men hur blir det med ?
Nu har du ju redan räknat ut men det kan vara bra att se att det finns en genväg också. Man kan nämligen skriva fältet så här
Och där kanske man till exempel känner igen och
Jaha okej hur tänker man med den där genvägen? Elr alltså jag förstår din omskrivning ibörjan men jag kör den långa vägen. Men jag kan absolut testa på ett separat papper och se om mitt svar är identiskt med genvägen. förresten hur ser du att (-y,x,0)=rsin(theta)phi?
Jag glömde att nämna att jag fick Ftheta=0 och Fphi=2Rsintheta
Så fältet blir alltså
Att kan man se genom att känna till att basvektorn uttrycks som
.
Nu när du har och kan du tillämpa formlerna för divergens och rotation. Du kan också utnyttja att samt att , vilket är ytterligare en genväg. Men räkna också på det "vanliga" sättet. Det är inte alltid man kan hitta genvägar.
D4NIEL skrev:Så fältet blir alltså
Att kan man se genom att känna till att basvektorn uttrycks som
.
Nu när du har och kan du tillämpa formlerna för divergens och rotation. Du kan också utnyttja att samt att , vilket är ytterligare en genväg. Men räkna också på det "vanliga" sättet. Det är inte alltid man kan hitta genvägar.
Hm jag har inte räknat på rotationen ännu men jag utnyttjade denna formel från formelsamling för div F och fick följande. Om du har fått div F till 3 så är mitt svar isåfall fel.
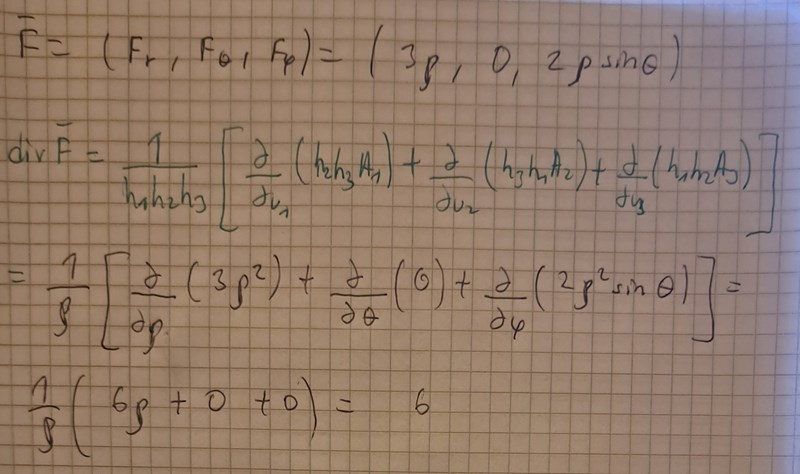
destiny99 skrev:D4NIEL skrev:Det är korrekt att blir , jättebra! Men hur blir det med ?
Nu har du ju redan räknat ut men det kan vara bra att se att det finns en genväg också. Man kan nämligen skriva fältet så här
Och där kanske man till exempel känner igen och
Jaha okej hur tänker man med den där genvägen? Elr alltså jag förstår din omskrivning ibörjan men jag kör den långa vägen. Men jag kan absolut testa på ett separat papper och se om mitt svar är identiskt med genvägen. förresten hur ser du att (-y,x,0)=rsin(theta)phi?
Du kan få fram det genom att utnyttja de inringade formlerna nedan.

Du har fått där det borde vara
Vidare ska du ha
Tänk på att
Visa spoiler
D4NIEL skrev:Du har fått där det borde vara
Vidare ska du ha
Tänk på att
Visa spoiler
Yes jag får nu som svar precis som dig. 
PATENTERAMERA skrev:destiny99 skrev:D4NIEL skrev:Det är korrekt att blir , jättebra! Men hur blir det med ?
Nu har du ju redan räknat ut men det kan vara bra att se att det finns en genväg också. Man kan nämligen skriva fältet så här
Och där kanske man till exempel känner igen och
Jaha okej hur tänker man med den där genvägen? Elr alltså jag förstår din omskrivning ibörjan men jag kör den långa vägen. Men jag kan absolut testa på ett separat papper och se om mitt svar är identiskt med genvägen. förresten hur ser du att (-y,x,0)=rsin(theta)phi?
Du kan få fram det genom att utnyttja de inringade formlerna nedan.
Ja ok då förstår jag.


