Tredjegradsekvation
Blir punkterna
Z1= 2(cos90+isin90)
Z2 = 2(cos210+isin210)
Z3 = 2(cos330+isin330)
?
Ska jag göra dem till formen a+bi sen och sätta in dem (x-z1)(x-z2)(x-z3) eller hur blir det?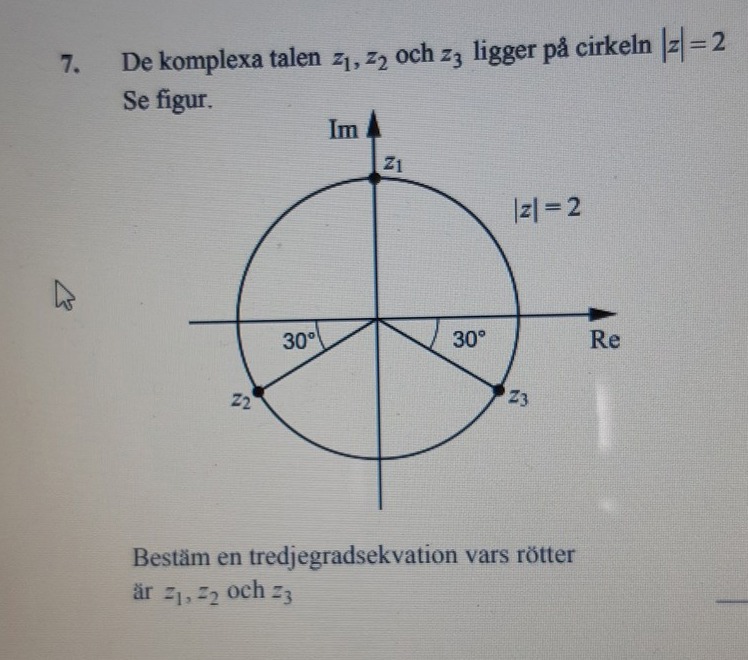
Nathal13 skrev:Blir punkterna
Z1= 2(cos90+isin90)
Z2 = 2(cos210+isin210)
Z3 = 2(cos330+isin330)
?
Ska jag göra dem till formen a+bi sen och sätta in dem (x-z1)(x-z2)(x-z3) eller hur blir det?
Ja det är ett sätt som fungerar.
Gör gärna så, så kan vi diskutera en annan metod sen
Ture skrev:Nathal13 skrev:Blir punkterna
Z1= 2(cos90+isin90)
Z2 = 2(cos210+isin210)
Z3 = 2(cos330+isin330)
?
Ska jag göra dem till formen a+bi sen och sätta in dem (x-z1)(x-z2)(x-z3) eller hur blir det?
Ja det är ett sätt som fungerar.
Gör gärna så, så kan vi diskutera en annan metod sen
Vad är den andra metoden?
Utnyttja deMoivres formel
antag att en ekvation ser ut så här:
z3 = w = a3(cos(3v)+isin(3v))
löser du den ekvationen får du att
z1 = a(cos(v)+isin(v)),
där v är pi/2 och a = 2
=>
z3 = 8e3pi/2 = -8i



