triangel

Hej

kan någon hjälpa mig med denna uppgift:

Låt a,b och c vara längder av sidorna i en triangel.

Visa att

$\frac{a + b}{a + b - c} + \frac{a + c}{a - b + c} + \frac{b + c}{- a + b + c} \geq 6$

När inträffar likhet?

Jag vet inte riktigt hur dem vill att man ska göra för att lösa uppgiften, ska man försöka få allt på en gemensamt bråkstreck så vi får en nämnare?

Börja med att fundera på den liksidiga triangeln där a = b = c. Vad får du för resultat då?

Multiplicera båda sidorna med var och en av nämnarna, så får du ett uttryck som inte är en kvot. Det brukar vara lättare att räkna med.

Tänk på att a, b och c måste vara strängt positiva- annars blir det ingen triangel.

Låt

$a = x + y, b = y + z, c = z + x .$

där $x, y, z > 0$ . Detta förenklar olikheten mycket, sedan är det bra att veta om att $w + \frac{1}{w} \geq 2$ för alla positiva w för att kunna färdigställa beviset. (Om man inte känner till det så är det en övning att bevisa det)

smaragdalena skrev :
Börja med att fundera på den liksidiga triangeln där a = b = c. Vad får du för resultat då?
Multiplicera båda sidorna med var och en av nämnarna, så får du ett uttryck som inte är en kvot. Det brukar vara lättare att räkna med.
Tänk på att a, b och c måste vara strängt positiva- annars blir det ingen triangel.

Okej, jag fick då $2 (a + b + c) \geq 6 (a + b - c) (a - b + c) (- a + b + c)$

Jursla skrev :
smaragdalena skrev :
Börja med att fundera på den liksidiga triangeln där a = b = c. Vad får du för resultat då?
Multiplicera båda sidorna med var och en av nämnarna, så får du ett uttryck som inte är en kvot. Det brukar vara lättare att räkna med.
Tänk på att a, b och c måste vara strängt positiva- annars blir det ingen triangel.
Okej, jag fick då $2 (a + b + c) \geq 6 (a + b - c) (a - b + c) (- a + b + c)$

Vad får du om du sätter a = b = c = 1 i ursprungsuttrycket?

Jursla skrev :
smaragdalena skrev :
Börja med att fundera på den liksidiga triangeln där a = b = c. Vad får du för resultat då?
Multiplicera båda sidorna med var och en av nämnarna, så får du ett uttryck som inte är en kvot. Det brukar vara lättare att räkna med.
Tänk på att a, b och c måste vara strängt positiva- annars blir det ingen triangel.
Okej, jag fick då $2 (a + b + c) \geq 6 (a + b - c) (a - b + c) (- a + b + c)$

Du har multiplicerat fel, det blir betydligt mer krångligt än sådär.

okej, jag är inte helt med på hur man ska göra för att komma vidare, är det meningen att man ska multiplicera ihop? även om det nu blev fel.

Jag tror att det är halvt hopplöst att försöka multiplicera ihop det. Utan använd följande istället, i en triangel kan man placera in en cirkel så att den tangerar alla sidor. Denna cirkel kommer att dela upp sidornas längder på följande sätt

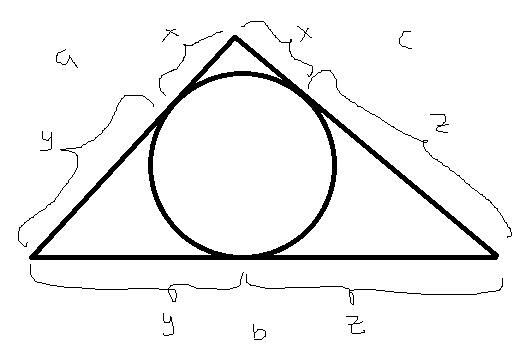
Detta betyder alltså att vi kan positiva reella tal x, y, z sådana att

$a = x + y, b = y + z, c = z + x$

Notera nu att

$a + b = x + 2 y + z, a + c = 2 x + y + z, b + c = x + y + 2 z, a + b - c = 2 y, a - b + c = 2 x, - a + b + c = 2 z$

Så sätter man in detta i VL i olikheten du ska bevisa så får man att

$\frac{x + 2 y + z}{2 y} + \frac{2 x + y + z}{2 x} + \frac{x + y + 2 z}{2 z} = 1 + \frac{x + z}{2 y} + 1 + \frac{y + z}{2 x} + 1 + \frac{x + y}{2 z} = 3 + \frac{1}{2} (\frac{x + z}{y} + \frac{y + z}{x} + \frac{x + y}{z}) = 3 + \frac{1}{2} (\frac{x}{y} + \frac{y}{x} + \frac{z}{y} + \frac{y}{z} + \frac{z}{x} + \frac{x}{z})$

Notera nu att vi har att

${(\sqrt{\frac{x}{y}} - \sqrt{\frac{y}{x}})}^{2} \geq 0 \Leftrightarrow \frac{x}{y} + \frac{y}{x} \geq 2$

Denna olikhet följer på precis samma sätt för summorna z/y + y/z och z/x + x/z också. Så det man får är att

$3 + \frac{1}{2} (\frac{x}{y} + \frac{y}{x} + \frac{z}{y} + \frac{y}{z} + \frac{z}{x} + \frac{x}{z}) \geq 3 + \frac{1}{2} (2 + 2 + 2) = 6$

och olikheten är visad. Som en övning så kan du ju gå igenom beviset och försöka förstå när likhet gäller.

Svara

Visa senaste svar