Triangel inskriven i större triangel
.jpg?width=800&upscale=false)
Problemet ovan försöker jag lösa men får fel svar. Jag har tänkt såhär:
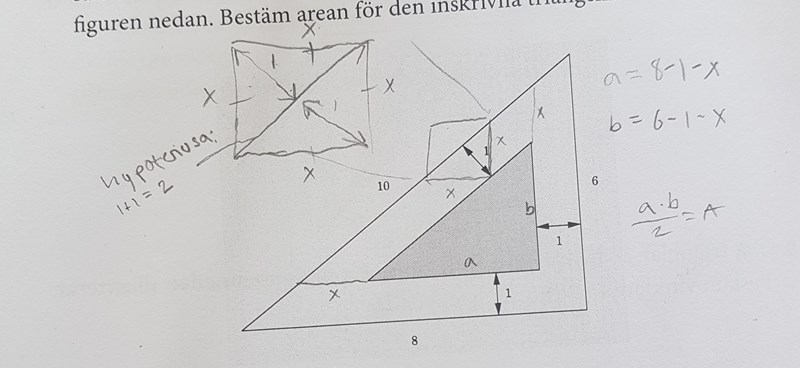
Med hjälp av Pythagoras sats fick jag att x var roten ur två och att arean var ungefär 10, men det stämmer inte med facit, vad har jag gjort fel?
Jag ser två fel.
1. De två sträckor du kallar x är inte lika långa.
2. Det stämmer inte att a + 1 + x = 8. Den sträcka som är 8 är längre än så.
Försökte lösa det med likformighet först men kom ingen vart så det var mest en chansning att de var lika långa... Skulle behöva hjälp med vart jag ska börja :S
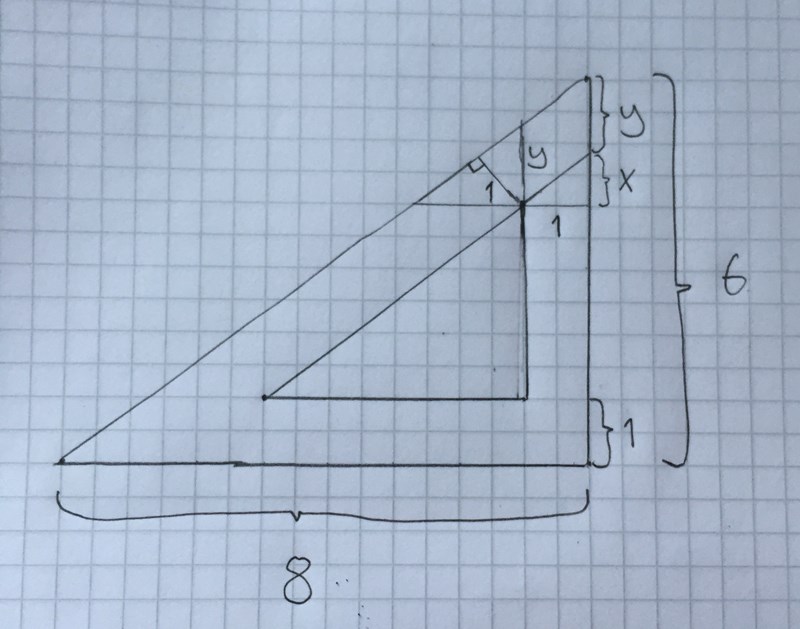
Det kanske finns ett enklare sätt, men detta är vad jag kom på. Om du kollar på bilden så behöver du beräkna två sträckor, x och y. x hittar du lätt med likformighet,
y är lite knepigare, men kolla på den lilla triangeln som bildas av mina hjälplinjer. Den är likformig med den stora., så vi kan skriva att , där h är höjden (dragen från hypotenusan) i den stora triangeln.
Men hur beräknar man h?, Jo den stora triangelns area är , men den är också .
Sedan får du göra likadant med den andra sidan.
Hej!
Eftersom den lilla triangelns sidor är parallella med stora triangelns sidor är trianglarna likformiga. Den lilla triangelns bas är och dess area är Den stora triangelns bas är och dess area är lika med Likformighet ger att areaskalan är lika med kvadraten på längdskalan, det vill säga
Albiki

