trig funktion
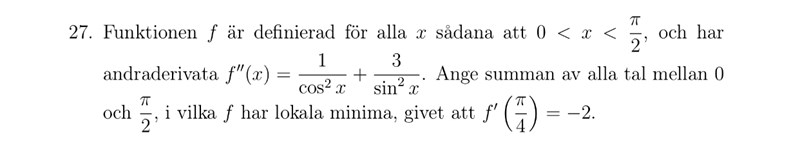 Svar pi/3
Svar pi/3
ingen aning hur man löser, vet knappt hur jag ska få ut antiderivatan
Okey vi ska börja någonstans. Vet du vad vi vill få fram?
Är du med på att du skall ta reda på derivatans nollställen och sedan undersöka om de är minimipunkter?
För att få fram kan kanske följande derivator vara till hjälp:
Är det här verkligen en Ma4-uppgift? /moderator
Antiderivata är ett annat namn på primitiv funktion - det står andraderivata.
Smaragdalena skrev:Är det här verkligen en Ma4-uppgift? /moderator
Frågan är från matematik- och fysikprovet år 2012 och proven kräver ma4 och fy2
Det första jag noterar är att det är onödigt att bestämma funktionen för att lösa uppgiften; det räcker att studera derivatan eftersom det är derivatans nollställen som är intressanta.
Kring ett lokalt minimum går från ett negativt värde till ett positivt värde då passerar från vänster till höger. Det betyder att kring ett lokalt minimum är en växande funktion, vilket säger att i närheten av ett lokalt minimum är andraderivatan positiv.
Du vet hur andraderivatan ser ut. För vilka är den positiv?
Egocarpo skrev:Okey vi ska börja någonstans. Vet du vad vi vill få fram?
Vi skall få fram alla lösningar i det givna intervallet som också är lokala minimipunkter (nollställen). Men hur ska jag få ut f’(x)? Förstår att man kan få fram nollställena via f’ men jag har ingen aning om hur man tar integralen av f”(x)
alvinB hade några bra idéer med derivator som är bra att kunna, prova att lösa dem!
Om man har en primitiv funktion kan man ju derviera den för att se om den var primitiven till funktionen som man började med.
Vart hittar du dem här uppgifterna någonstans?





