Trig räknerglerna

Vet inte hur jag tar mig vidare härifrån 

Är ej sant

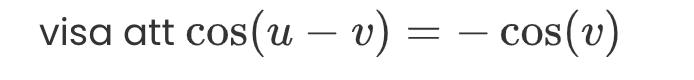
Sätt t.ex. v=0 => cos(u)=-1 för alla u?

Jag gissar att det står $\pi$ i uppgiften där du har skrivit u.

Laguna skrev:

Jag gissar att det står $\pi$ i uppgiften där du har skrivit u.

Då har du gissat fel

Då får du visa en bild av uppgiften.

Arup skrev:

Då har du gissat fel

Påståendet $\cos(u-v) = -\cos v$ är inte sant för alla vinklar $u$ och $v$. Vill du visa att påståendet stämmer, så kommer du misslyckas!

Däremot är $\cos(\pi - v) = -\cos v$ sant för alla vinklar $v$.

Laguna skrev:

Då får du visa en bild av uppgiften.

OK. Kan du börja om då?

Jag vet ej hur jag ska börja. 

Vad var problemet med inlägg# 3 ?

Om du är med på att det ska vara pi och inte u, så är inlägg 3 och 4 alldeles utmärkta. 

Arup skrev:

Jag vet ej hur jag ska börja. 

Vad var problemet med inlägg# 3 ?

Är det 1237 eller 1236 som du vill lösa?

Arup skrev:

Laguna skrev:

Då får du visa en bild av uppgiften.

VAd får du med formeln för cos(u-v) om du sätter u = 0 ?

DVS utvecklar cos(0-v)

då blir det cos(-v)=cos(v)

Tillägg: 11 sep 2025 19:15

Kan jag tänka cos(-1*v) och förenkla mha räknereglerna ?

Arup skrev:

 

---

Tillägg: 11 sep 2025 19:15

Kan jag tänka cos(-1*v) och förenkla mha räknereglerna ?

Hur menar du då?

Ture skrev:

Arup skrev:

 

---

Tillägg: 11 sep 2025 19:15

Kan jag tänka cos(-1*v) och förenkla mha räknereglerna ?

Hur menar du då?

Jag undrar ifall man skulle kunna använda den här regeln om vi har cos(1×-v)

Tanken är nog att du ska göra så här:

Enligt formeln så är cos(u-v) = cos(u)cos(v)+sin(u)sin(v) för alla vinklar u och v.

Speciellt för u = 0° så får vi cos(0°-v) =cos(0°)cos(v)+sin(0°)sin(v) = 1•cos(v)+0•sin(v) = cos(v).

Eftersom cos(0°-v) = cos(-v) så har vi att cos(-v) = cos(v)

Detta gäller för alla vinklar v, och alltså även om vi kallar vinkeln v för u, vilket ger oss det önskade cos(-u) = cos(u).