Trig uppgift från NP

Varför blir det här fel ?

Så nu fick jag rätt svar. Men, jag undrar varför den 1:a metoden inte gav mig samma svar.

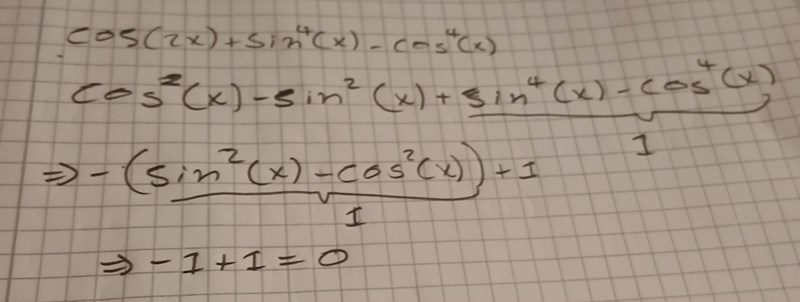
Arup skrev:

Så nu fick jag rätt svar. Men, jag undrar varför den 1:a metoden inte gav mig samma svar.

Kan du förklara hur du tänkte med första metoden?

Eller åtminstone skriva ut fler räknesteg?

Det är lite svårt att följa din lösning.

Yngve skrev:

Arup skrev:

Så nu fick jag rätt svar. Men, jag undrar varför den 1:a metoden inte gav mig samma svar.

Kan du förklara hur du tänkte med första metoden?

Eller åtminstone skriva ut fler räknesteg?

Det är lite svårt att följa din lösning.

Jag kan använda trig 1:an för ${\sin }^4\left(x\right)-{\cos }^4\left(x\right)=1$

och cossinus för dubbla vinklen kan skrivas om som :

$\cos \left(2x\right)=2{\cos }^2\left(x\right)-1$

summerar vi dessa får vi :

$$\begin{gathered} 2 {\cos }^2\left(x\right)-1+1 \\ =2{\cos }^2\left(x\right) \end{gathered}$$eller hur ?

Trig:ettan lyder $\sin^2 x + \cos^2 x = 1$.

Notera då att $\sin^4 x - \cos^4 x \ne 1$

Arup skrev:

Jag kan använda trig 1:an för ${\sin }^4\left(x\right)-{\cos }^4\left(x\right)=1$

Nej, det stämmer inte.

Men du kan göra så här om du vill:

$\sin^4(x)-\cos^4(x)$

= (konjugatregeln) =

$(\sin^2(x)-\cos^2(x))(\sin^2(x)+\cos^2(x))$

= (trigettan) =

$(\sin^2(x)-\cos^2(x))\cdot1=\sin^2(x)-\cos^2(x)$

Jag måste ha blandat plus(+) med minus(-)

Arup skrev:

Jag måste ha blandat plus(+) med minus(-)

OK, men det gäller inte heller att sin⁴(x)+cos⁴(x) = 1.

Kontrollera gärna själv med räknaren.

Eller välj x = 45°, vilket ger de kända sinus- och cosinusvärdena sin(45°) = cos(45°) = $\frac{1}{\sqrt{2}}$ och räkna för hand.

Yngve skrev:

Arup skrev:

Jag måste ha blandat plus(+) med minus(-)

OK, men det gäller inte heller att sin⁴(x)+cos⁴(x) = 1.

Kontrollera gärna själv med räknaren.

Eller välj x = 45°, vilket ger de kända sinus- och cosinusvärdena sin(45°) = cos(45°) = $\frac{1}{\sqrt{2}}$ och räkna för hand.

varför gäller inte att ${\sin }^4\left(x\right)+{\cos }^4\left(x\right) =1 ?$

Det här kommer ju från tig ettan

På vilket sätt kommer det från trigettan?

Provade du Yngves exempel?

Arup skrev:

varför gäller inte att ${\sin }^4\left(x\right)+{\cos }^4\left(x\right) =1 ?$

Det är jättebra att du försöker se mönster i materialet och att du formulerar egna samband.

Men det är då jätteviktigt att du provtrycker/rimlighetskontrollerar dina teorier på något sätt innan du börjar använda dem.

I det här fallet:

Du vet (från formelbladet) att

1) sin²(x)+cos²(x) = 1.

Din teori är att det även ska gälla att

2) sin⁴(x)+cos⁴(x) = 1.

Nu måste du testa din teori innan du använder den.

Här är ett förslag på hur du kan göra det:

Om du sätter ihop 1) och 2) så får du ekvationen/sambandet

3) sin²(x)+cos²(x) = sin⁴(x)+cos⁴(x)

Vi kan nu titta på de specialfall för vilka vi vet att sambandet gäller, nämligen 

sin(x) = $\pm$1, vilket ger cos(x) = 0 och därför att 1+0 = 1+0, dvs 1 = 1.

cos(x) = $\pm$1, vilket ger sin(x) = 0 och därför att 0+1 = 0+1, dvs 1 = 1.

Men för alla andra värden på sin(x) och cos(x) så gäller att både sin²(x) och cos²(x) är positiva tal som är mindre än 1

Det betyder att både sin⁴(x) och cos⁴(x) är ännu mindre positiva tal.

Därför måste det gälla att sin²(x)+cos²(x).>.sin⁴(x)+cos⁴(x).

Hängde du med?

Yngve skrev:

Arup skrev:

varför gäller inte att ${\sin }^4\left(x\right)+{\cos }^4\left(x\right) =1 ?$

Det är jättebra att du försöker se mönster i materialet och att du formulerar egna samband.

Men det är då jätteviktigt att du provtrycker/rimlighetskontrollerar dina teorier på något sätt innan du börjar använda dem.

I det här fallet:

Du vet (från formelbladet) att

1) sin²(x)+cos²(x) = 1.

Din teori är att det även ska gälla att

2) sin⁴(x)+cos⁴(x) = 1.

Nu måste du testa din teori innan du använder den.

Här är ett förslag på hur du kan göra det:

Om du sätter ihop 1) och 2) så får du ekvationen/sambandet

3) sin²(x)+cos²(x) = sin⁴(x)+cos⁴(x)

Vi kan nu titta på de specialfall för vilka vi vet att sambandet gäller, nämligen 

sin(x) = $\pm$1, vilket ger cos(x) = 0 och därför att 1+0 = 1+0, dvs 1 = 1.

cos(x) = $\pm$1, vilket ger sin(x) = 0 och därför att 0+1 = 0+1, dvs 1 = 1.

Men för alla andra värden på sin(x) och cos(x) så gäller att både sin²(x) och cos²(x) är positiva tal som är mindre än 1

Det betyder att både sin⁴(x) och cos⁴(x) är ännu mindre positiva tal.

Därför måste det gälla att sin²(x)+cos²(x).>.sin⁴(x)+cos⁴(x).

Hängde du med?

Nej

Om ett tal är mindre än 1 ( men positivt)

a < 1

så är talet gånger sig själv mindre än talet gånger 1

a * a < a * 1

Är du med på det?

Exempel:

Om a² = 0,6 så är a⁴ = 0,36, vilket är mindre än 0,6.

Pröva gärna även med andra tal.

vi kan ju väl uttrycka ${\sin }^4\left(x\right)=({\sin }^2{\left(x\right))}^2$

Ja.

För säkerhets skull vill jag ställa en fråga till Arup då jag har en gissning om vad som är problemet i diskussionen ovan.

Du vet väl att likheten $(A + B)^2 = A^2 + B^2$ inte är sann, eller? (bortsett från undantagsfallet där ett av talen A eller B är noll)

Därmed är sambandet $(\sin^2 x + \cos^2 x)^2 = \sin^4 x + \cos^4 x$ inte heller sant.

LuMa07 skrev:

För säkerhets skull vill jag ställa en fråga till Arup då jag har en gissning om vad som är problemet i diskussionen ovan.

Du vet väl att likheten $(A + B)^2 = A^2 + B^2$ inte är sann, eller? (bortsett från undantagsfallet där ett av talen A eller B är noll)

Därmed är sambandet $(\sin^2 x + \cos^2 x)^2 = \sin^4 x + \cos^4 x$ inte heller sant.

Ja, det stämmer enligt kvadreringsreglerna..