Trigonometiska ekvationer

ingetmattesnille skrev:

Hej!

Jag har en fundering kring en ekvation.

$\sin \frac{x}{3}=\frac{\sqrt{3}}{2}$

Min uträkning är:

Lösning 1:

$\sin \frac{x}{3}=\frac{2\mathrm{\pi }}{3}$

Multiplicerar med 3 på bägge sidor

$\sin x = 2\mathrm{\pi }$

 

Lösning 2:

$\sin \frac{x}{3}=\frac{\mathrm{\pi }}{3}$

Multiplicerar återigen med 3 på bägge sidor

$\sin x = \mathrm{\pi }$

 

 

Har jag tänkt rätt?

Du har gjort några fel.

Dels missar du periodiciteten, dels så blandar du ihop funktion och argument det är inte sin(x/3) som är 2pi/3 utan x/3 som är pi/3. (Du gjorde både ett formellt och ett sifferfel här)

Vi har:

$\sin \left(\frac{x}{3}\right) =\frac{\sqrt{3}}{2}$

För att lösa den tar vi arcsin av bägge led (kallas även för sin^-1)

Eftersom sin(v) = sin(pi-v) får vi två möjliga fall

fall 1: $\frac{x}{3}= \frac{\pi }{3} +2n\pi$ (Viktigt att ha med periodiciteten)

som vi kan förenkla till

x = $\pi$ + 6n$\pi$

där n är ett godtyckligt heltal

Fall 2: $\frac{x}{3}=\pi -\frac{\pi }{3}+2n\pi$

kan du fortsätta härifrån på egen hand?

Ture skrev:

ingetmattesnille skrev:

Hej!

Jag har en fundering kring en ekvation.

$\sin \frac{x}{3}=\frac{\sqrt{3}}{2}$

Min uträkning är:

Lösning 1:

$\sin \frac{x}{3}=\frac{2\mathrm{\pi }}{3}$

Multiplicerar med 3 på bägge sidor

$\sin x = 2\mathrm{\pi }$

 

Lösning 2:

$\sin \frac{x}{3}=\frac{\mathrm{\pi }}{3}$

Multiplicerar återigen med 3 på bägge sidor

$\sin x = \mathrm{\pi }$

 

 

Har jag tänkt rätt?

Du har gjort några fel.

Dels missar du periodiciteten, dels så blandar du ihop funktion och argument det är inte sin(x/3) som är 2pi/3 utan x/3 som är pi/3. (Du gjorde både ett formellt och ett sifferfel här)

Vi har:

$\sin \left(\frac{x}{3}\right) =\frac{\sqrt{3}}{2}$

För att lösa den tar vi arcsin av bägge led (kallas även för sin^-1)

Eftersom sin(v) = sin(pi-v) får vi två möjliga fall

fall 1: $\frac{x}{3}= \frac{\pi }{3} +2n\pi$ (Viktigt att ha med periodiciteten)

som vi kan förenkla till

x = $\pi$ + 6n$\pi$

där n är ett godtyckligt heltal

Fall 2: $\frac{x}{3}=\pi -\frac{\pi }{3}+2n\pi$

kan du fortsätta härifrån på egen hand?

Tack för din tid!

"För att lösa den tar vi arcsin av bägge led (kallas även för sin-1)

Eftersom sin(v) = sin(pi-v) får vi två möjliga fall"

Dessa förstår jag inte, jag vet att jag använder mig av arcsin för att få ut graderna från en trigonometrisk ekvation, men inte riktigt hur jag använder mig av det här.

Skulle du också kunna förklara sin(v) = sin(pi-v) och varför det ger två möjliga utfall?

Helt ärligt är jag inte heller säker på vilka misstag jag gjort, då jag nyss börjat med denna kurs.

Jag kikade i formelbladet för trigonometriska funktionsvärden, där jag såg att 3√/2 blev i radianer både 2π/3 och π/3. Hur kommer det sig att vi bara använder den senare radianen?

Jag förstår dock din uträkning i Fall 1.

Fall 2 borde bli

X = 3π - π + 6nπ

X = 8nπ , stämmer det?

"För att lösa den tar vi arcsin av bägge led (kallas även för sin-1)"

Tänk ekvationen $\sin v = \frac{1}{2}$

Denna löser du enkelt genom att ta $v = {\sin }^{-1}\left(\frac{1}{2}\right)={30}^{°}$där ${30}^{°}=\frac{\mathrm{\pi }}{6}$ i radianer.

Nu låt oss säga att $\sin \left(\frac{v}{2}\right)= \frac{1}{2}$ , denna löser man på exakt samma sätt där du kan se hela $\frac{v}{2}$ som en egen variabel.

När du tar ${\sin }^{-1}$ blir det därför av hela kvoten $\frac{v}{2}$ och då måste hela uttrycket vara lika med $\frac{v}{2}=\frac{\pi }{6}$.

"Eftersom sin(v) = sin(pi-v) får vi två möjliga fall"

Precis, detta kan man förklara med hjälp av Enhetscirkeln som du måste förstå innan du kan förstå dig på det jag kommer förklara nu.

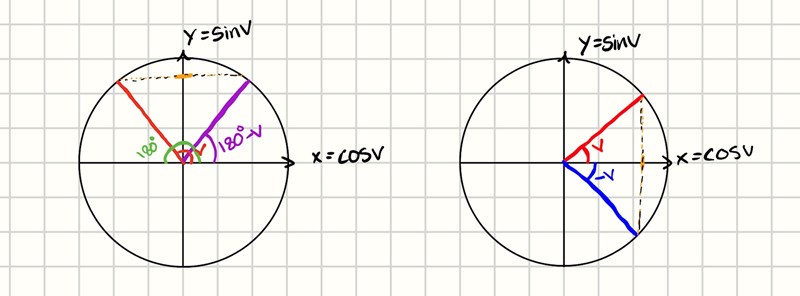
I figuren till vänster kan vi se att $\sin v$, alltså y-axeln antar samma värden vid två olika lägen som passaren har vridits från den positiva x-axeln (vid två olika vinklar alltså). Först vid vinkeln v och sedan vinkeln ${180}^{°}-v$.

Därför är inte lösningarna som jag skrev längre upp inte fullständiga då vi endast har kommit fram till vinkeln v som var lika med $\frac{\pi }{6}$radianer. Men det finns även en till vinkeln som ger samma värde på y-axeln som vi finner vid $\pi -\frac{\pi }{6}$där $\pi$ är detsamma som ${180}^{°}$.

Sedan måste vi även lägga till $+ n2\pi$ då samma värden på y kan antas när passaren vrider sig ett helt varv ( ${360}^{°}=2\pi$).

Ungefär samma sak gäller även vid cosinusekvationer. Kan du komma fram till hur samtliga lösningar ser ut då? T.ex till ekvationen $\cos v =\frac{1}{2}$. Du kan använda dig av figuren till höger som ledtråd.

Ett till tips är att kolla så att du kan byta mellan grader och radianer i din räknare för då fås svaret direkt i radianer, i räknaren alltså (om du inte gjort det än såklart).

X = 8nπ , stämmer det?

Inte riktigt, det blir $x=2\pi + n6\pi$

då du inte kan addera $(3\pi -\pi )$med $n6\pi$ då det innehåller ett n