trigonometreiskt uttryck
Hur räknar man ut detta utan räknare?
Testade att utveckla med sinus additionsformel, Men det blev inte lättare
Om man fuskar litet och räknar ut det så får man att arctan(5) + arctan(3/2) är 135 grader.
Om det är till någon hjälp vet jag inte.
Jo det hjälper, 45+90=135
Men jag har inte fått en sån ledtråd.
En oprövad ide,
Arctan5 = arcsin(5/260,5)
PPå samma sätt kan man uttrycka vinkeln som arccos(1/260, 5)
GGör samma med den andra vinkeln
Slutligen, summaformeln för sin
Gö lik
Jag skulle ta tan av summan, alltså använda summaformeln för tan.
@Ture - Hur vet du att den likheten gäller? Jag tror inte det är tänkt att man ska göra så dock. Jag vet inte vad som är tänkt
@Laguna - Ja, även om jag gör det. Hur hjälper det när jag har arctan ?
Hur blir det om du provar?
Laguna skrev:Hur blir det om du provar?
Jag tänker att:
Hmm, om jag förstår rätt är tanken nu att använda att tan(v+u)=-1 Och det är ekvivalent med vilken vinkel som helst som ger -1?
Så tillbaks till ursprungsuttrycket
Tillägg: 28 mar 2024 11:42
Jag tänker nog lite fel. tan(u+v)=-1 betyder inte att sin(u+v)=-1
Laguna skrev:Jag skulle ta tan av summan, alltså använda summaformeln för tan.
Det är betydligt enklare om man kommer ihåg den, vilket jag inte gör.
Korra skrev:@Ture - Hur vet du att den likheten gäller? Jag tror inte det är tänkt att man ska göra så dock. Jag vet inte vad som är tänkt
Rita upp en rätvinklig triangel med kateterna 5 och 1
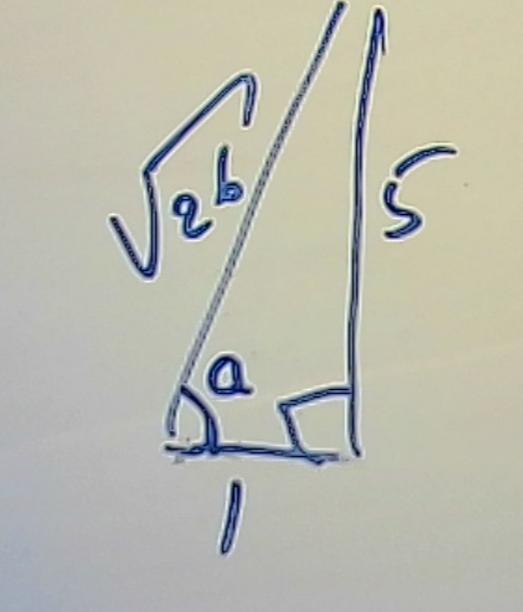
tan(a) blir givetvis 5 och hypotenusan bestämmer vi med pytagoras till
då inser man att sin(a) =
och därför är vinkeln a = arcsin()
osv
Jan Ragnar skrev:
Tror inte det förväntas att man ska göra så, men jag gillar det. Det är smart
Tack så mycket, förstår





.jpg?width=800&upscale=false)
