Trigonometri

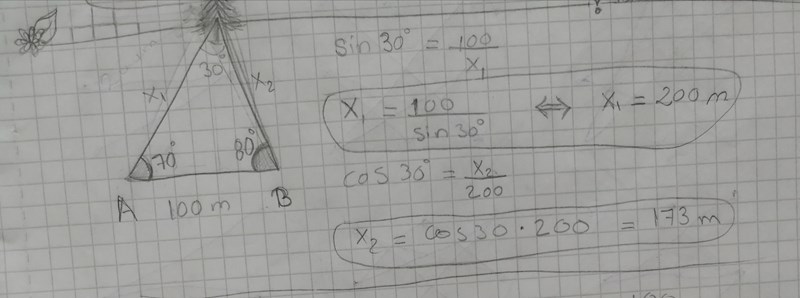
Goddag
Har ingen facit.. Stämmer mina beräkningar?
Nej,
De samband du använt gäller enbart rätvinkliga trianglar.
I det här fallet är det lämpligt att använda sinussatsen
Ture skrev:Nej,
De samband du använt gäller enbart rätvinkliga trianglar.
I det här fallet är det lämpligt att använda sinussatsen
Aha tack...
Jag tror jag fick nu rätt värde på avståndet mellan trädet och lantmätare A, men inte på det andra. Varför det?

Ekvationerna har du ställt upp helt riktigt.
Men sedan har du satt in hela den andra ekvationen som högerled till den första. Därefter har du ersatt det med lösningen till den andra ekvationen (dvs 197,96). Det kan inte stämma. Högerledet till den första ekvationen är ju fortfarande 0,005.
Jag tror skrivsättet (sin70°)/a = (sin80°)/b = 0,005 har varit förvillande.
Det är säkrare att sedan skriva ut ekvationerna var och en för sig:
(sin70°)/a = 0,005 som ger a.
(sin80°)/b = 0,005 som ger b ≈ 196,96 (som du löste på vägen).
Arktos skrev:Ekvationerna har du ställt upp helt riktigt.
Men sedan har du satt in hela den andra ekvationen som högerled till den första. Därefter har du ersatt det med lösningen till den andra ekvationen (dvs 197,96). Det kan inte stämma. Högerledet till den första ekvationen är ju fortfarande 0,005.
Jag tror skrivsättet (sin70°)/a = (sin80°)/b = 0,005 har varit förvillande.
Det är säkrare att sedan skriva ut ekvationerna var och en för sig:(sin70°)/a = 0,005 som ger a.
(sin80°)/b = 0,005 som ger b ≈ 196,96 (som du löste på vägen).
Aha... Slarv fel.. Tack för hjälp
Tror det ska stämma nu




