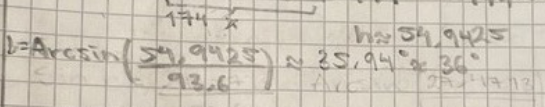Trigonometri - beräkna en triangels vinklar
Hej! Jag har stött på en uppgift inom trigonometri där det finns två rätta svar, fast jag har bara kommit på lösningen till ett av dem. Därför skulle jag vilja ha hjälp med förstå hur man kan tänka för att komma fram till de båda svaren. Frågan lyder: ”Två av sidorna i en triangel med arean 0,478 m2 är 174 cm och 93,6 cm. Bestäm triangelns vinkar, svara i hela grader.”
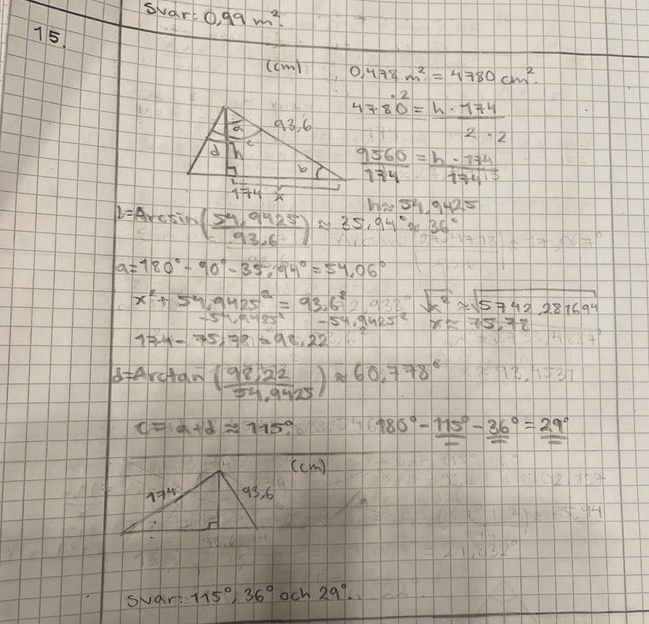
Jag bifogar min lösning nedan som gav svaret 115 grader, 36 grader och 29 grader. Jag ber om ursäkt för att lösningen är ganska rörig och otydlig, men jag hoppas ändå att det kan vara till hjälp! :) Jag började helt enkelt med att använda arean och en av sidorna i triangeln för att beräkna höjden. Med hjälp av detta kunde jag sedan räkna ut vinklarna genom att använda mig de rätvinkliga trianglarna som bildades inom triangeln.
I facit fanns det sedan ett ytterligare svar där vinkarna skulle vara 144 grader, 24 grader och 12 grader. Jag lyckas dock inte lista ut hur jag ska komma fram till detta. Min tanke är att ingen av givna sidorna då utgör basen av triangeln, eftersom det skulle ge samma svar som vinkarna i den tidigare triangeln. Är det så? Isåfall vet jag inte hur jag ska ta mig vidare eftersom jag inte förstår hur jag ska använda mig av arean i triangeln.
Känner du till areasatsen? Den ger dig två möhliga värden på en av vinklarna.
Cosinussatsen ger dig sen den sista sidan.
Ture skrev:Känner du till areasatsen? Den ger dig två möhliga värden på en av vinklarna.
Cosinussatsen ger dig sen den sista sidan.
Nej, det gör jag tyvärr inte
Ok, du har fått fram att arcsin av ett uttryck är ca 36 grader. Bra det, men du missar att det finns en lösning till, nämligen 180-36 = 144 vilket ger den andra lösningen
Detta eftersom sin(x) = sin(180-x)
Ture skrev:Ok, du har fått fram att arcsin av ett uttryck är ca 36 grader. Bra det, men du missar att det finns en lösning till, nämligen 180-36 = 144 vilket ger den andra lösningen
Detta eftersom sin(x) = sin(180-x)
Förlåt, men jag hänger inte riktigt med😅 Jag har inte arbetat med den regeln förut tyvärr, men då vet jag iallafall hur jag ska gå tillväga! Tack!
Ture skrev:Ok, du har fått fram att arcsin av ett uttryck är ca 36 grader. Bra det, men du missar att det finns en lösning till, nämligen 180-36 = 144 vilket ger den andra lösningen
Detta eftersom sin(x) = sin(180-x)
Men kommer den andra lösningen till triangeln se ut så som jag tänkte? Alltså att ingen av de givna sidorna utgör basen av triangeln? För visst skulle triangeln annars få samma vinkar som den första lösningen, även om man byter plats på 174 cm och 93,6 cm?
Tyra_S skrev:Ture skrev:Ok, du har fått fram att arcsin av ett uttryck är ca 36 grader. Bra det, men du missar att det finns en lösning till, nämligen 180-36 = 144 vilket ger den andra lösningen
Detta eftersom sin(x) = sin(180-x)
Men kommer den andra lösningen till triangeln se ut så som jag tänkte? Alltså att ingen av de givna sidorna utgör basen av triangeln? För visst skulle triangeln annars få samma vinkar som den första lösningen, även om man byter plats på 174 cm och 93,6 cm?
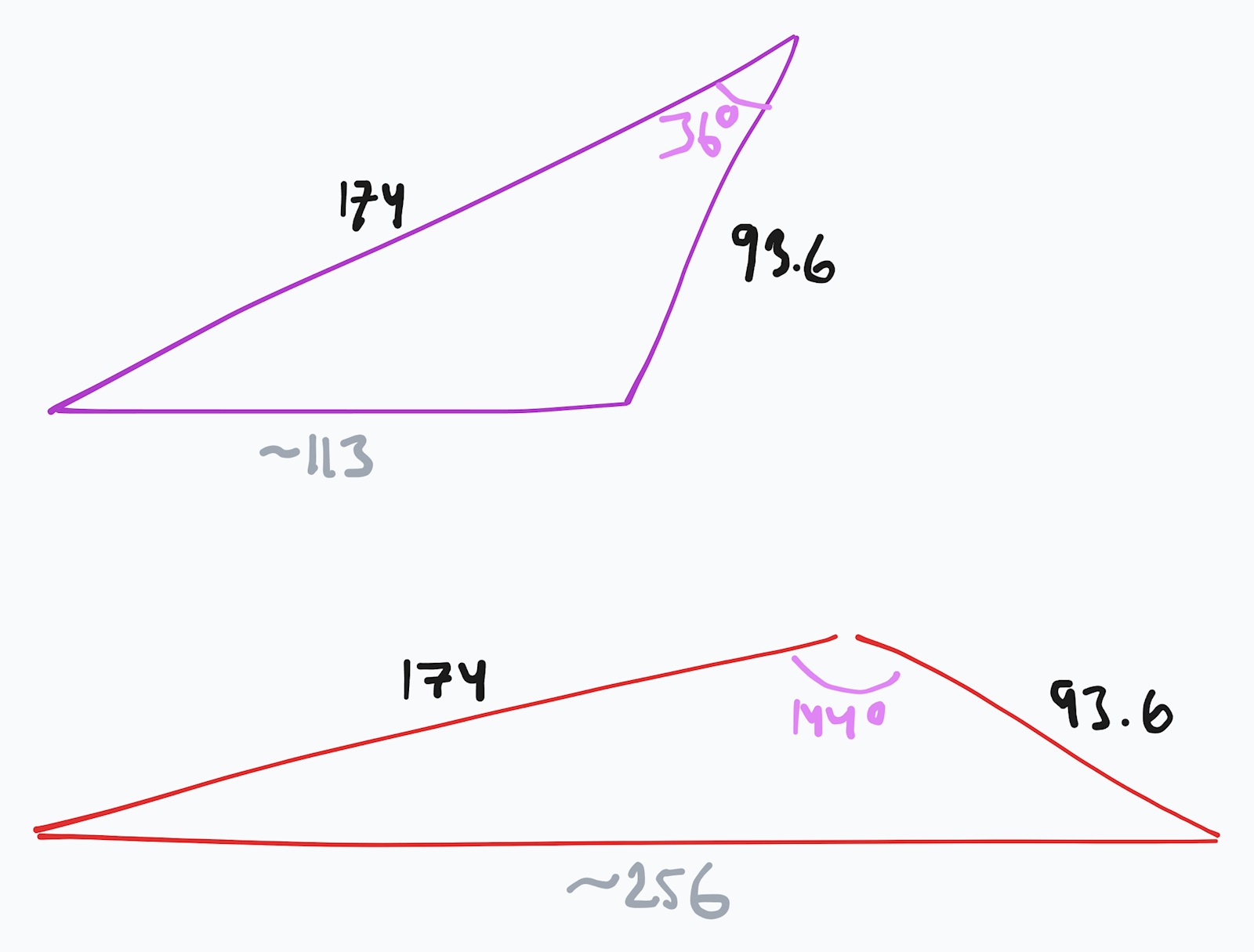
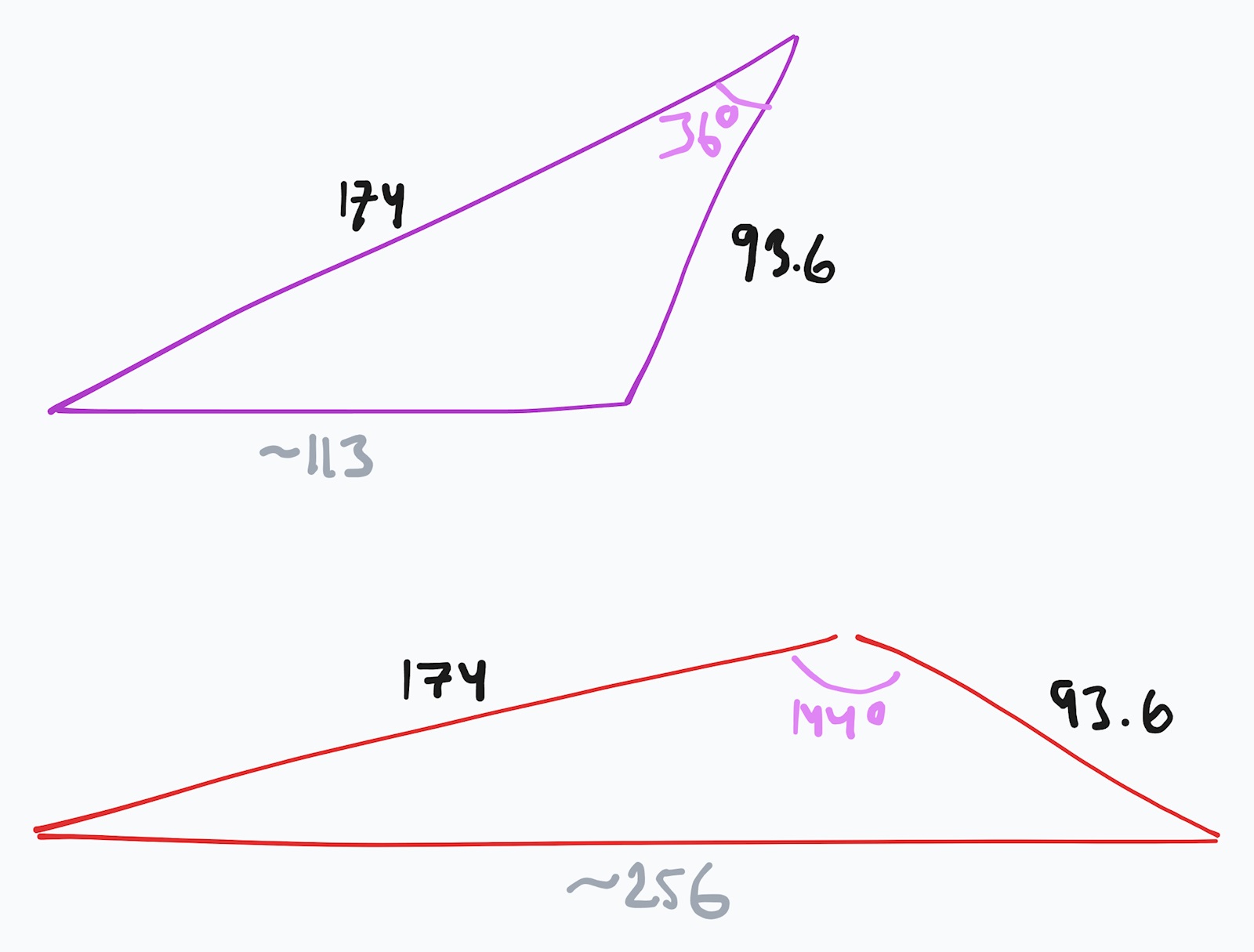
Det stämmer att ingen av de två givna sidorna utgör basen i triangeln, inte i någon av dem. Fast det beror ju på hur du vänder dem förstås.
Hur som helst stämmer inte din ritning med den korrekta vinkel du beräknat.
Så här ser de ut. Först den med din vinkel och därefter den andra som Ture tipsade om.
sictransit skrev:Tyra_S skrev:Ture skrev:Ok, du har fått fram att arcsin av ett uttryck är ca 36 grader. Bra det, men du missar att det finns en lösning till, nämligen 180-36 = 144 vilket ger den andra lösningen
Detta eftersom sin(x) = sin(180-x)
Men kommer den andra lösningen till triangeln se ut så som jag tänkte? Alltså att ingen av de givna sidorna utgör basen av triangeln? För visst skulle triangeln annars få samma vinkar som den första lösningen, även om man byter plats på 174 cm och 93,6 cm?
Det stämmer att ingen av de två givna sidorna utgör basen i triangeln, inte i någon av dem. Fast det beror ju på hur du vänder dem förstås.
Hur som helst stämmer inte din ritning med den korrekta vinkel du beräknat.
Så här ser de ut. Först den med din vinkel och därefter den andra som Ture tipsade om.
Tack! Förlåt, jag har en sista fråga bara! Finns det något annat sätt att beräkna att vinkeln är 144 grader utan att använda areasatsen, eftersom jag inte har lärt mig om den ännu?
Jo det går
du hade i ditt första inlägg den här ekvationen
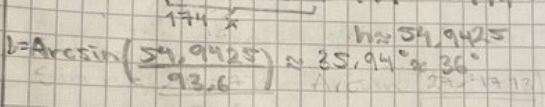
Den ekvationen har två lösningar
Dels 36 grader, som du räknade vidare från, men den har också lösningen
144 grader (= 180 - 36)
Så räknar du vidare även med det fallet får du det andra fallet.
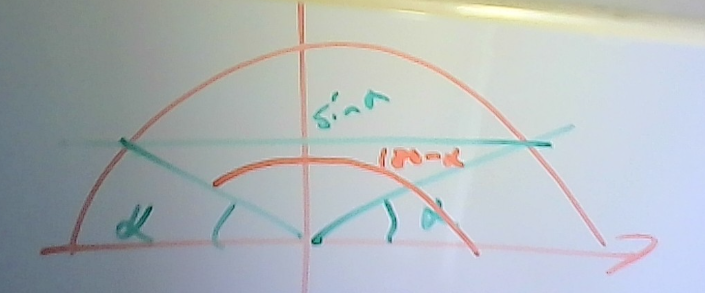
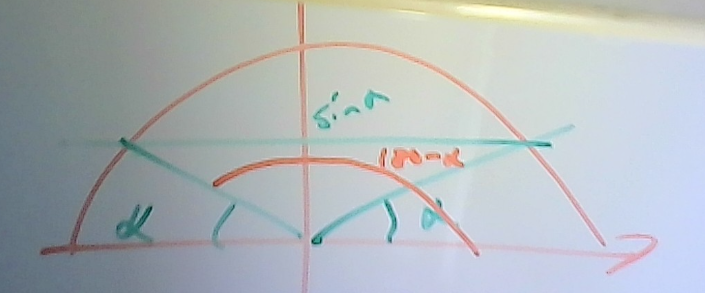
att sin(a) = sin(180-a) ser man dels i sitt formelblad men också (och bättre) i enhetscirkeln
Därför har arcsin(x) två lösningar
Ture skrev:Jo det går
du hade i ditt första inlägg den här ekvationen
Den ekvationen har två lösningar
Dels 36 grader, som du räknade vidare från, men den har också lösningen
144 grader (= 180 - 36)
Så räknar du vidare även med det fallet får du det andra fallet.
att sin(a) = sin(180-a) ser man dels i sitt formelblad men också (och bättre) i enhetscirkeln
Därför har arcsin(x) två lösningar
Tack för hjälpen!
Tyra_S skrevTack för hjälpen!
Tips: Leta upp Enhetscirkeln i din bok eller på nätet och lär dig hur den kan användas i trigonometriska sammanhang.