Trigonometri kluringar
Hej, behöver hjälp med en typ av prblem som jag inte verkar kunna greppa. Jag lägger upp ett par exemple av den typen i hopp om att någon kan klar göra det för mig, tack på förhand.
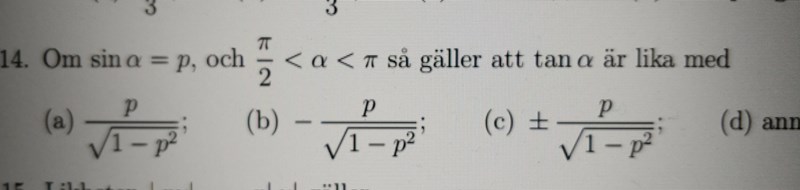
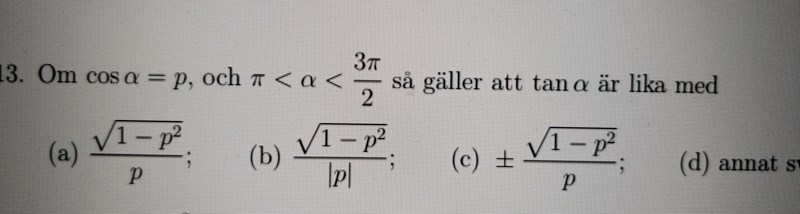
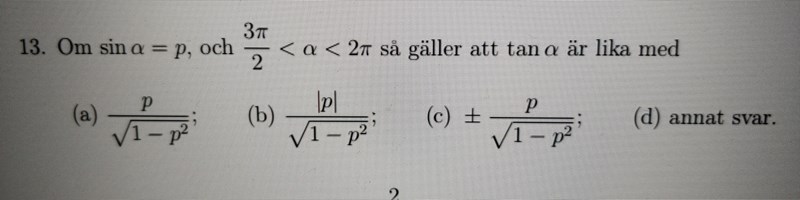
Ursäkta antalet, men själva uträkning är inga konstigheter utan anledningen till tecken som svaret har och i vissa fall även absolut belopp.
Svar 1: b
Svar 2: a
Svar 3: b
Alla dessa handlar om att kombinera sin/cos definitionen av tan och trigonometriska ettan.
SeriousCephalopod skrev:Alla dessa handlar om att kombinera sin/cos definitionen av tan och trigonometriska ettan.
Skulle du kunna utveckla? Jag förstår att man använder sig utav trigonometriska ettan och sin/cos, men förstår inte varför svaret är (a) och inte (b) i sista bilden till exempel, och även andra bilden där svaret är (b) istället för (a). Jag lyckas inte finna sambandet/regeln. Jag har använt enhetscirkeln för att hitta något svar men har inte lyckats hitta något som gäller generellt för denna typen av frågor.
**
Svar 1: b
Svar 2: b
Svar 3: a
Grunden är enhetscirkeln. Om vi tar uppgift 13 t.ex. så är det fjärde kvadranten och eftersom
måste det gälla att .
I fjärde kvadranten är även , vilket innebär att b) måste vara fel, för det ger att .
mo14 skrev:
...
Jag har använt enhetscirkeln för att hitta något svar men har inte lyckats hitta något som gäller generellt för denna typen av frågor.
Enhetscirkeln ger dig följande:
- I första kvadranten är både sinus och cosinus positiva, vilket gör att tangens är positiv.
- I andra kvadranten är sinus positiv och cosinus negativ, vilket gör att tangens är negativ.
- I tredje kvadranten är både sinus och cosinus negativa, vilket gör att tangens är positiv.
- I fjärde kvadranten är sinus negativ och cosinus positiv, vilket gör att tangens är negativ.
Nyckeln är att rita enhetscirkeln så att man kan titta i den vad som är positivt och vad som är negativt. Jag visar i tre steg hur jag skulle göra:
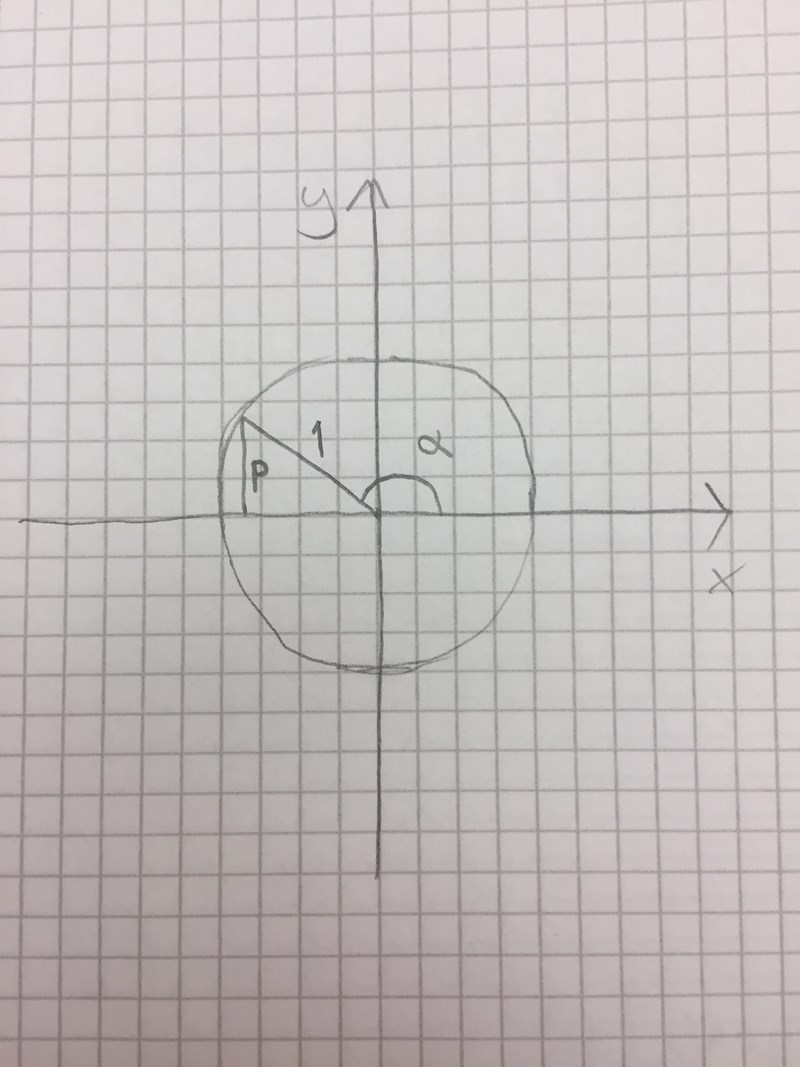
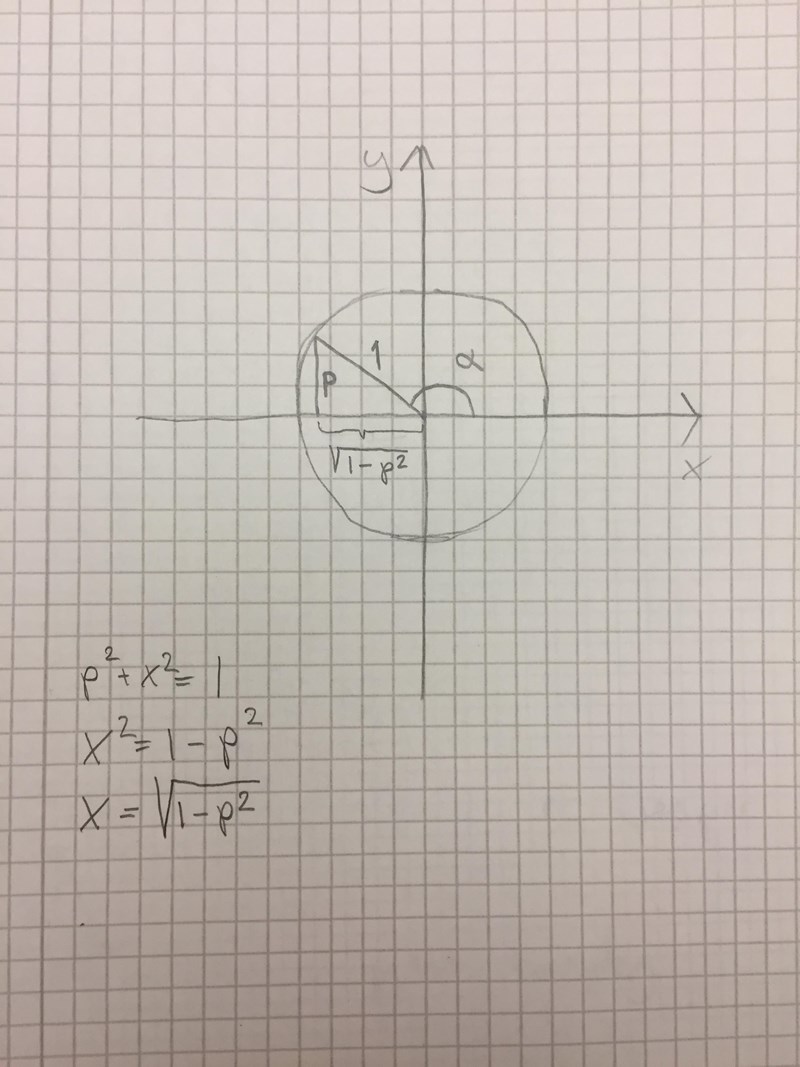
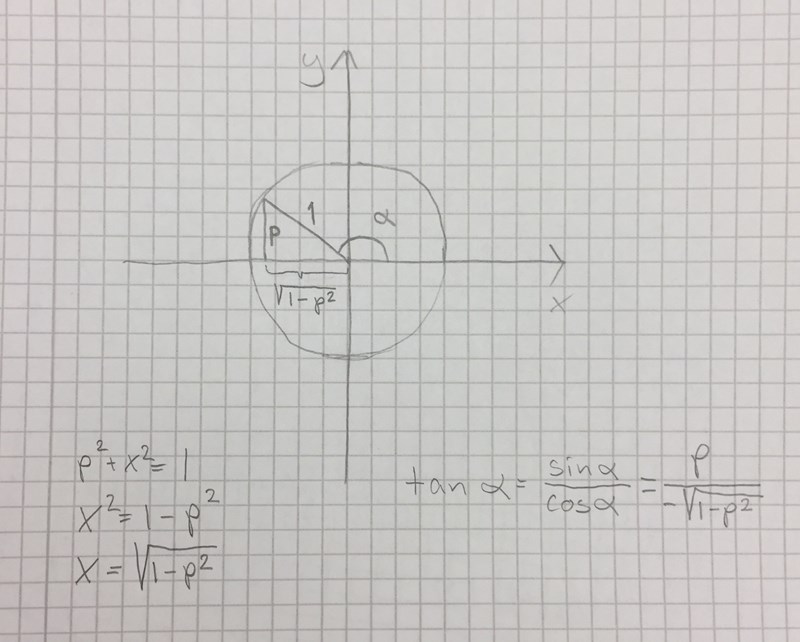
Ser bra ut! Det luriga är när . Då får man kalla sträckan för för att få ihop det.
Tack för all hjälp! Nu är det mycket klarare i huvudet!




