Trigonometri - likformighet matte 1c
Hej!
Förstår inte hur jag ska lösa uppgift 7206 uppgift b)
Hur ska man ställa upp på enklast sätt för att se att trianglarna är likformiga? Själva uträkningen för x är enkel, men jag har lite svårt att se hur trianglarna är likformiga.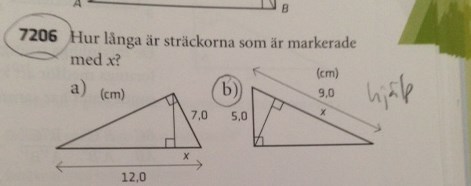
Se har 2 vinklar som är lika. (vilket ger att även den 3:e är lik)
På b har du 3 trianglar. De är alla likformiga men de har inte samma vinklar gemensam.
Den största och mellantriangeln har en 90 graders vinkel och den vinkeln som är längst ner till höger.
Den minsta triangeln och den största har 90 gradersvinkel och den längst upp till vänster.
Lite svårare är kanske att se att den minsta triangeln är likformig med mellantriangeln men det går.
trianglar är likformiga om samtliga vinklar är lika.
I detta fall är en vinkel gemensam och en vinkel är 90 grader i vardera triangeln, alltså måste även den tredje vinkeln vara lika.
Således är trianglarna likformiga!
REsonemanget ovan gäller för de två största trianglarna, när man konstaterat det kan man applicera samma resonemang för den tredje lilla triangeln
Ture skrev :trianglar är likformiga om samtliga vinklar är lika.
I detta fall är en vinkel gemensam och en vinkel är 90 grader i vardera triangeln, alltså måste även den tredje vinkeln vara lika.
Således är trianglarna likformiga!
REsonemanget ovan gäller för de två största trianglarna, när man konstaterat det kan man applicera samma resonemang för den tredje lilla triangeln
Jag tror att jag förstår men hur ska man rita upp dessa tre trianglar för att komma fram till vad x är ? Jag tror att det blir lättare att räkna ut x om man ställer upp de likformiga trianglarna.
Hur menar du med rita upp?
Du kan annars tänka så här:
Trianglarna är likformiga. Då gäller att den korta kateten delat med hypotenusan blir samma för båda trianglarna.
Du har en liten triangel där korta kateten är x och hypotenusan 7.
Sedan en stor triangel där den korta kateten är 7 och hypotenusan 12.
x/7 = 7/12
SvanteR skrev :Hur menar du med rita upp?
Du kan annars tänka så här:
Trianglarna är likformiga. Då gäller att den korta kateten delat med hypotenusan blir samma för båda trianglarna.
Du har en liten triangel där korta kateten är x och hypotenusan 7.
Sedan en stor triangel där den korta kateten är 7 och hypotenusan 12.
x/7 = 7/12
Jag har löst fråga a) korrekt, det är fråga b) som jag inte förstår.
Rita tre trianglar bredvid varandra, alla med den spetsigaste vinkeln åt vänster och hypotenusan neråt (exempelvis). Sätt ut de mått du känner till (du vet ju två sidor på den största triangeln och en på vardera av de små trianglarna).
Hej!
Om två trianglar har samma vinklar så är de likformiga.
Om två rätvinkliga trianglar har samma två spetsiga vinklar så är trianglarna likformiga.
Uppgift b.
Den stora triangeln har hörnen A, B, och C (moturs med start vid toppen). Den har vinklarna 90, BAC och ACB.
Den lilla triangeln har hörnen A, B och D (moturs med start vid toppen). Den har vinklarna 90, BAC och ABD.
Den mellanstora triangeln har hörnen D, B och C. Den har vinklarna 90, ACB och DBC.
Eftersom så är , vilket visar att den stora triangeln och den lilla triangeln är likformiga.
Eftersom så är , vilket visar att den stora triangeln och den mellanstora triangeln är likformiga.
Samtliga tre rätvinkliga trianglar i figuren är tydligen likformiga.
Albiki





