Trigonometri - vad är sidan x?

Vi kan börja med att rita in höjden 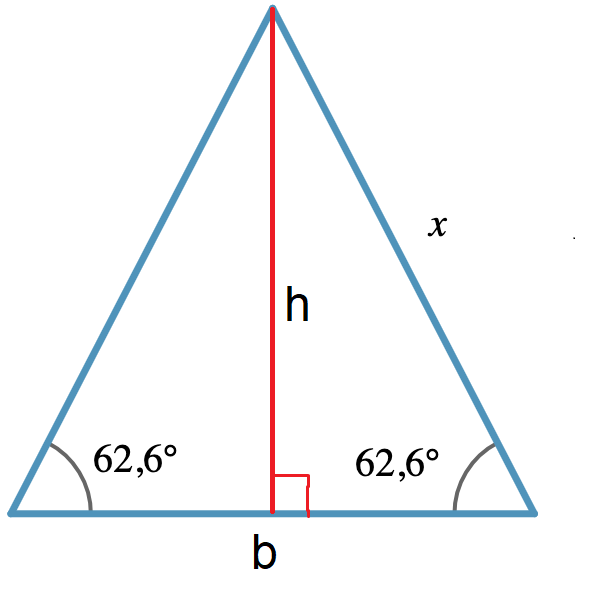$h$. 

Kan vi ställa upp ett uttryck för arean av denna triangel? Ser du, med hjälp av den rätvinkliga triangeln i bilden, något samband mellan $h$ och $x$?

ja arean blir då (x*h)/2. och h kan räknas ut genom pythagoras, ${(0.5x)}^2+h^2=x^2$ vilket innebär att $h^2=0.75x^2 alltså h=\sqrt{0.75}\times x$.

kan jag med det ge arean ett nytt uttryck? x*h/2 --> $\frac{x\times \sqrt{0.75}\times x}{2}$ alltså $\frac{x^2\times \sqrt{0.75}}{2}$?

hur hjälper denna information mig dock?

h_09 skrev:

ja arean blir då (x*h)/2. och h kan räknas ut genom pythagoras, ${(0.5x)}^2+h^2=x^2$ vilket innebär att $h^2=0.75x^2 alltså h=\sqrt{0.75}\times x$.

kan jag med det ge arean ett nytt uttryck? x*h/2 --> $\frac{x\times \sqrt{0.75}\times x}{2}$ alltså $\frac{x^2\times \sqrt{0.75}}{2}$?

hur hjälper denna information mig dock?

Jag tänkte lite fel i min bild, sorry! Basen har inte längd $x$, råkade anta det av någon anledning. Aja, iden är fortfarande densamma. Om vi kallar basen istället för $b$ ger dina uträkningar att 

Arean $A = \frac 12 bh$
Förhållande mellan $x$, $h$ och $b$ med pythagoras: $x^2 = (\frac 12 b)^2 + h^2$. 
Det finns ett sista förhållande mellan $x$ och $h$ med hjälp av trigonometri, vilket?

cos 54.8 = h/x ??

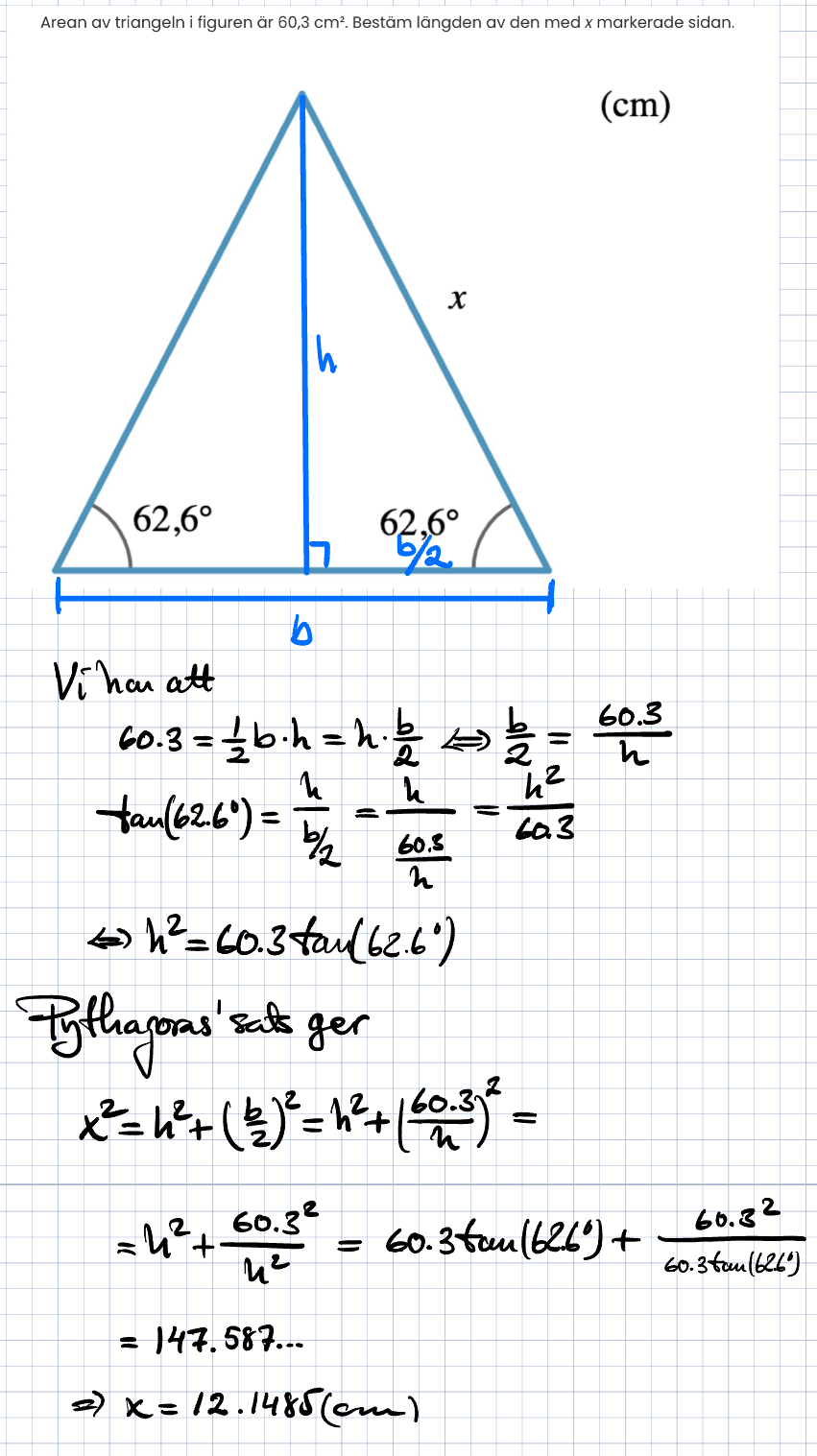
Åh herregud, varför var det så mycket??

Jag tror nog jag förstår ändå, ska försöka lösa uppgiften själv senare för att se om det sitter. Tack för förklaringen!

Det är jättenyttigt att kunna lösa den med pythagoras och lite trigonometri, så skippa inte tipsen ovan.

Sedan kan du kika efter areasatsen i din formelsamling: $A=\frac{bc\times \sin \alpha }{2}$

Se till att du förstår den, så det inte bara blir mekaniskt räknande. Beviset är förstås snarlikt vad som redan skrivits i den här tråden.

Arean A är given i uppgiften, b=c=x och toppvinkeln α har du ju redan räknat ut.

Lös för x.

Klart!

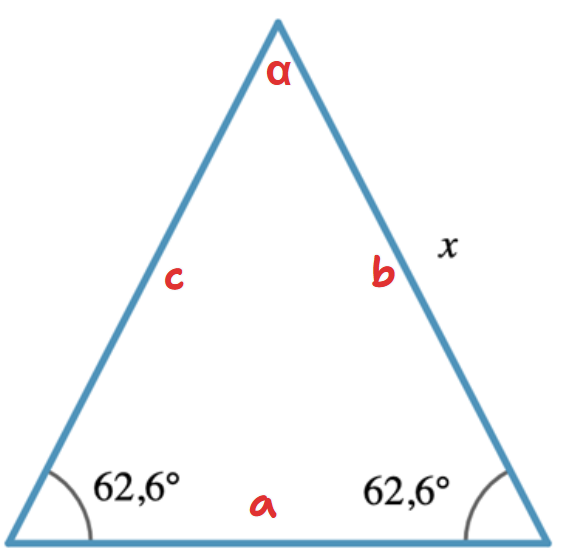
Jag har aldrig sett areasatsen, den finns inte heller i mitt formelblad.

h_09 skrev:

Jag har aldrig sett areasatsen, den finns inte heller i mitt formelblad.

Då har i alla fall sett den nu. Användbar om du har två sidor och mellanliggande vinkel. 

h_09 skrev:

Jag har aldrig sett areasatsen, den finns inte heller i mitt formelblad.

Den kan vara mycket användbar. Den kommer ofta upp i matte 3, där gör man lite mer trigonometri utöver det som gör i ma1. 

https://www.matteboken.se/lektioner/gymnasiet/matte-fortsattning-niva-1/trigonometri/areasatsen#!/

Konstig länk, jag hittade den under Matte 3.

A, den verkar iallafall lite överkurs eftersom man knappt möter trigonometri i matte 1, och inget utöver sin cos tan och pythagoras

Jo, lite kanske, men man behöver inte kunna mer än sinus och den klassiska formeln för triangelns area. Inte ens pythagoras är nödvändig att använda.

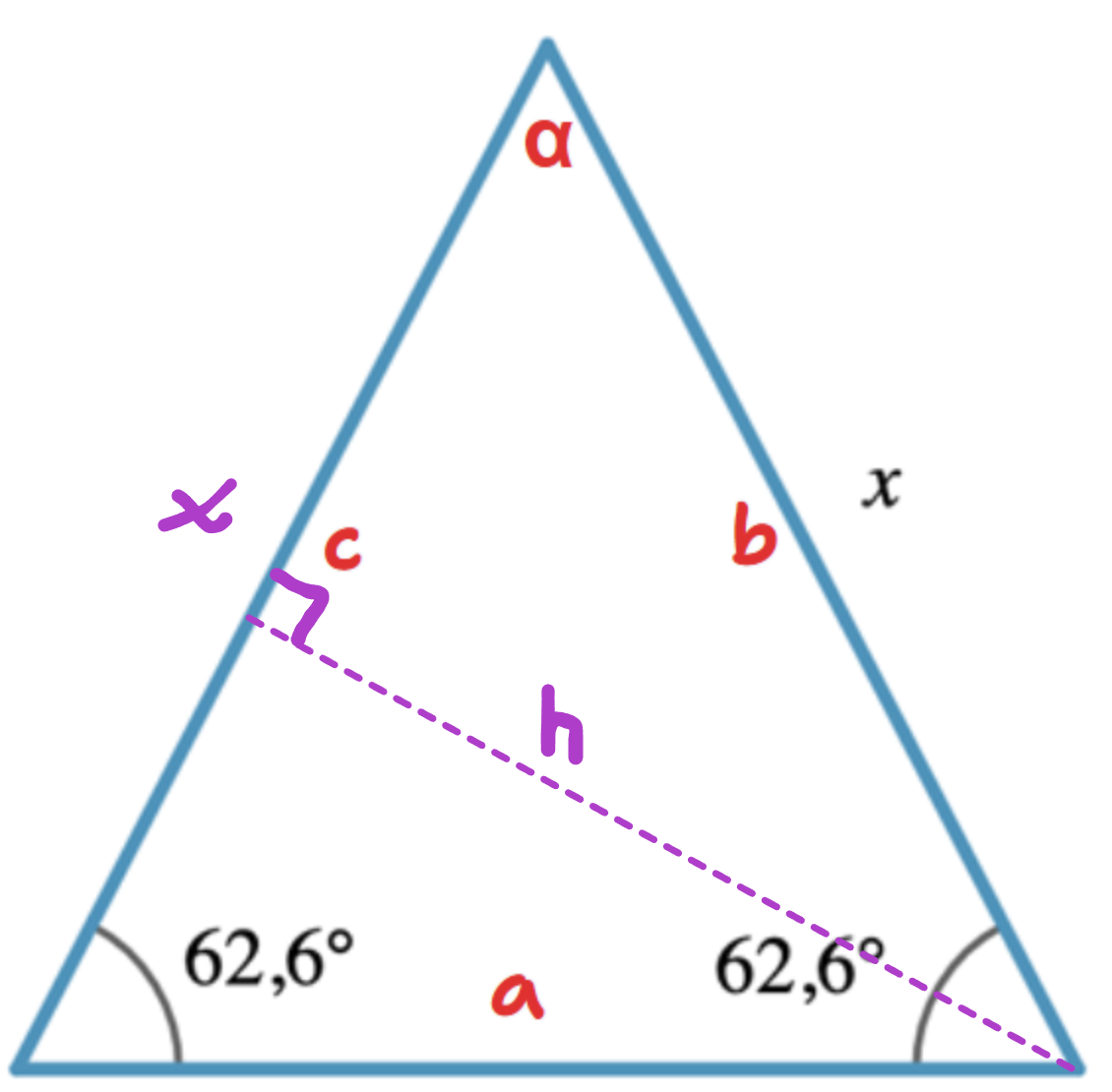
Jag har ritat in en annan höjd h mot en bas som är x.

Vi vet att $A=\frac{bh}{2}$. Basen i det här fallet är x, så vi får: $A=\frac{xh}{2}$.

Höjden h vet vi inte hur lång den är, men vi vet att sin(α) är "motstående genom hypotenusan".

Det ger oss: $\sin \alpha =\frac{h}{x}$

Jag vill ha ett uttryck för h så jag kan ersätta det i areaformeln:

$\sin \alpha =\frac{h}{x} \Rightarrow h=x\sin \alpha$

$$\begin{gathered} A=\frac{xh}{2}; h=x\sin \alpha \Rightarrow \\ A=\frac{x^2\sin \alpha }{2} \end{gathered}$$

Nu kan jag sätta in α=54,8° samt A=60,3 cm² och lösa för x.

$$\begin{gathered} 60,3=\frac{x^2\sin 54,8}{2} \\ x=\sqrt{\frac{2\times 60,3}{\sin 54,8}}\approx 12,1 \mathrm{cm} \end{gathered}$$

Åh! Jag fattar!! Det tar lite tänkande men man kan ju komma dit även om man inte har satsen i huvudet. Det var bra att förstå, tack så mycket!