Trigonometri - vad är vinkeln a?

Hej, har denna uppgift:

Ett parallellogram är inskrivet i en kvadrat så som figuren visar. Parallellogrammets area är en tredjedel av kvadratens area. Bestäm vinkeln a.

Jag är osäker vart jag ska börja.

Kvadrat area: $x^{2}$

Parallellogram area: $\frac{x^{2}}{3}$ eller (basen * höjden)

arcsin x/b = a

hur ska jag få fram sambandet mellan x och b (basen?)

Notera att höjden av parallellogrammet är $x$ . Om basen är $b$ , så ska $bx = \frac{x^2}{3}$ .

Gustor skrev:
Notera att höjden av parallellogrammet är $x$ . Om basen är $b$ , så ska $bx = \frac{x^2}{3}$ .

Men observera också att ni två använder olika beteckningar. I din ansats h_09 betecknar du den långa sidan på parallellogrammet som "basen b". Gustor betecknar den korta sidan på parallellogrammet som "basen b".

Sant, jag kan skriva om det till $b x = \frac{x^{2}}{3}$

men hur hjälper det mig?

Jag förenklade snabbt bx= x^2/3 till 3b=x. Men är detta relevant info?

Ja, det är relevant. Om du fortsätter med den nya beteckningen på paralellogrammets bas, så ser du att det trigonometriska förhållandet till vinkeln alfa istället blir

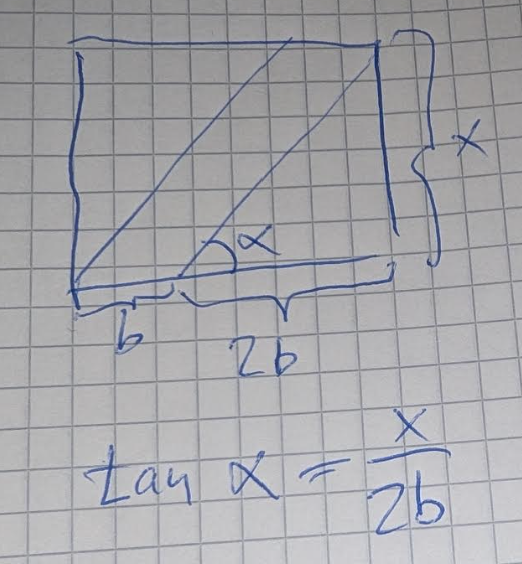
Ser du hur det kan bli såhär?

Yes! I så fall blir väl arctan 3b/2b vilket blir ungefär 56.3 grader. Då är det vinkeln a. Är det korrekt?

Det verkar rimligt. Det ska bli mer än 45°, eller hur?

Ja, det ska bli mer än 45 eftersom a är mindre spetsig än vinkeln på toppen av triangeln. Och jag fick fram facit, det är korrekt. Tack för hjälpen!!

JohanF skrev:
Gustor skrev:
Notera att höjden av parallellogrammet är $x$ . Om basen är $b$ , så ska $bx = \frac{x^2}{3}$ .

Men observera också att ni två använder olika beteckningar. I din ansats h_09 betecknar du den långa sidan på parallellogrammet som "basen b". Gustor betecknar den korta sidan på parallellogrammet som "basen b".

Sorry, skrev lite hastigt och kollade inte så noga.

Gustor skrev:
JohanF skrev:
Gustor skrev:
Notera att höjden av parallellogrammet är $x$ . Om basen är $b$ , så ska $bx = \frac{x^2}{3}$ .

Men observera också att ni två använder olika beteckningar. I din ansats h_09 betecknar du den långa sidan på parallellogrammet som "basen b". Gustor betecknar den korta sidan på parallellogrammet som "basen b".

Sorry, skrev lite hastigt och kollade inte så noga.

Jag tyckte att det blev jättebra! Visar hur viktigt det är att försöka välja beteckningar som gör beräkningsstegen så "straight forward" som möjligt. Man hade ju kommit i mål med den ursprungliga ansatsen också, men det var kanske inte lika uppenbart utan hade krävt något beräkningssteg extra.

Svara

Visa senaste svar