Trigonometri - vad blir fel?

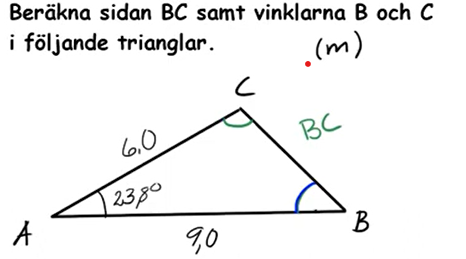
Kan du visa hur du gjort? 

Felet verkar ligga här, det ska inte vara ett minusstecken på värdet av 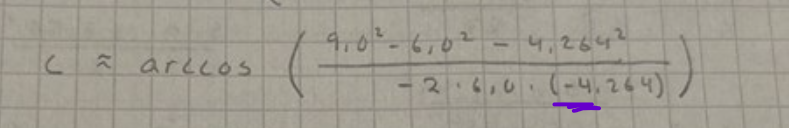$BC$ (då $BC>0$).

Verkar ge ett rimligare värde på vinkeln 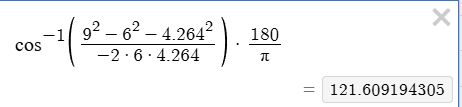$C$

Jadu, verkar som att jag helt missade. Jag har ju själv skrivit att BC ungefär är 4,264. Såg resten bra ut?

Ja, det ser bra ut! Om du vill ha en extra koll att allt är rätt kan du använda sinussatsen för att verifiera värdet på vinklarna $B$ och $C$. 

Men, jag tänte på en annan sak. Borde inte jag få två lösningar? Alltså om jag använder sinussatsen?

Ja, det stämmer faktiskt. Jag har inte gjort sådana här frågor på en rätt lång tid. Min intuitiva gissning är att, eftersom vi kommer få två par lösningar för $B$ och $C$, finns bara en av dem som adderar upp till rätt vinkelsumma. Men sinussatsen är en bra metod bara att verifiera att din lösning stämmer, du behöver inte nödvändigtvis lösa allt på nytt. Det räcker att kolla om

$\displaystyle \frac{\sin C}{|AB|} = \frac{\sin B}{|AC|} = \frac{\sin A}{|BC|}$

Jo, men precis. Jag tänkte mest om jag valde sinussatsen från början. Då hade jag fått två lösningar. Vad är det då som gör att jag ska välja bort den andra och säga att den ena stämmer. Och om jag inte räknat fel, blir vinkelsumman att stämma.

Abcd1000 skrev:

Jo, men precis. Jag tänkte mest om jag valde sinussatsen från början. Då hade jag fått två lösningar. Vad är det då som gör att jag ska välja bort den andra och säga att den ena stämmer. Och om jag inte räknat fel, blir vinkelsumman att stämma.

Det blir nog lite krångligare. Sinussatsen ger 

$B \approx 145.4^\circ$ (fall 1)
$B\approx 34.6^\circ$ (fall 2)

I fall 1 får vi enligt vinkelsumman i en triangel att $C \approx 10.8^\circ$
Här kan du testa om sinussatsen är uppfylld, det kommer den inte att vara ($\sin(C)/|AB| \neq \sin(B)/|AC|$). På så sätt får vi att detta inte är en lösning.

Ja, det är därför jag föredrar att använda cosinussatsen för den ger väl bara ett svar och alltså det rätta?

Abcd1000 skrev:

Ja, det är därför jag föredrar att använda cosinussatsen för den ger väl bara ett svar och alltså det rätta?

Ja, den bör alltid ge ett svar. 

Tackar verkligen för hjälpen!