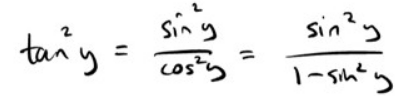trigonometrisk ekvation

Skriv alla tre ingående delar i HL som bråk.

Bubo skrev:

Skriv alla tre ingående delar i HL som bråk.

Förlåt uttryckte mig fel

Härledning finns på raden direkt ovanför den likhet du frågar om:

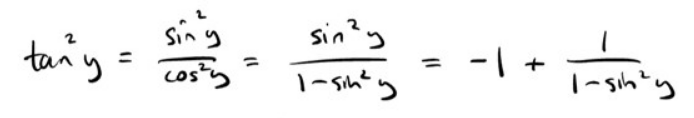
Man började med definitionen av tangens som kvoten av sinus- och cosinusvärdena. Sedan tillämpades trigonometriska ettan och till slut lade man till en etta och tog bort den för att kunna utföra division:

$\dfrac{\sin^2 y}{1-\sin^2y} = \dfrac{\sin^2 y - 1 + 1}{1-\sin^2y} = \dfrac{\sin^2 y - 1}{1-\sin^2y} + \dfrac{1}{1-\sin^2y} = -1 + \dfrac{1}{1-\sin^2y}$

Nu har man alltså kommit fram till likheten  $\tan^2 y = -1 + \dfrac{1}{1-\sin^2y}$.  Det återstår att flytta över ettan från HL till VL och sedan vända på bråken:

$\dfrac{\tan^2 y + 1}{1} = \dfrac{1}{1-\sin^2y}$ ger $\dfrac{1}{\tan^2 y + 1} = \dfrac{1-\sin^2y}{1}$

Alternativ metod:

När man skrivit om tan²y enligt

så är det bara att lösa ut sin² y.

$\tan^2 y = \dfrac{\sin^2 y}{1-\sin^2 y}$

multiplicera båda leden med (1-sin²y):
$\iff (1-\sin^2 y) \tan^2 y = \sin^2 y$

skriv ut produkten i VL:
$\iff \tan^2 y - \sin^2y \tan^2y = \sin^2 y$

samla alla termer med sin² y på högerledet:
$\iff \tan^2 y = \sin^2y \tan^2y + \sin^2 y$

bryt ut sin² y:
$\iff \tan^2 y = \sin^2y (\tan^2y + 1)$

dividera båda leden med (tan²y+1):
$\iff \dfrac{\tan^2 y}{1+\tan^2 y} = \sin^2 y$

Det är egentligen denna likhet som senare använts i uträkningen

LuMa07 skrev:

Härledning finns på raden direkt ovanför den likhet du frågar om:

Man började med definitionen av tangens som kvoten av sinus- och cosinusvärdena. Sedan tillämpades trigonometriska ettan och till slut lade man till en etta och tog bort den för att kunna utföra division:

$\dfrac{\sin^2 y}{1-\sin^2y} = \dfrac{\sin^2 y - 1 + 1}{1-\sin^2y} = \dfrac{\sin^2 y - 1}{1-\sin^2y} + \dfrac{1}{1-\sin^2y} = -1 + \dfrac{1}{1-\sin^2y}$

Nu har man alltså kommit fram till likheten  $\tan^2 y = -1 + \dfrac{1}{1-\sin^2y}$.  Det återstår att flytta över ettan från HL till VL och sedan vända på bråken:

$\dfrac{\tan^2 y + 1}{1} = \dfrac{1}{1-\sin^2y}$ ger $\dfrac{1}{\tan^2 y + 1} = \dfrac{1-\sin^2y}{1}$

---

Alternativ metod:

När man skrivit om tan²y enligt

så är det bara att lösa ut sin² y.

$\tan^2 y = \dfrac{\sin^2 y}{1-\sin^2 y}$

multiplicera båda leden med (1-sin²y):
$\iff (1-\sin^2 y) \tan^2 y = \sin^2 y$

skriv ut produkten i VL:
$\iff \tan^2 y - \sin^2y \tan^2y = \sin^2 y$

samla alla termer med sin² y på högerledet:
$\iff \tan^2 y = \sin^2y \tan^2y + \sin^2 y$

bryt ut sin² y:
$\iff \tan^2 y = \sin^2y (\tan^2y + 1)$

dividera båda leden med (tan²y+1):
$\iff \dfrac{\tan^2 y}{1+\tan^2 y} = \sin^2 y$

Det är egentligen denna likhet som senare använts i uträkningen

tack!