Trigonometrisk ekvation
Hej, ska lösa denna ekvation:
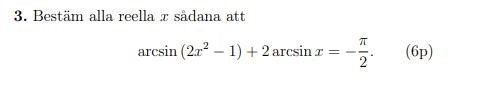
Jag ansätter först följande:
Detta resulterar i att:
Om vi substituerar dessa uttryck i den första ekvationen erhålls:
Vilket blir min lösning. Problemet uppstår sedan när jag skissar funktionen för uttrycket i VL i första ekvationen och får:
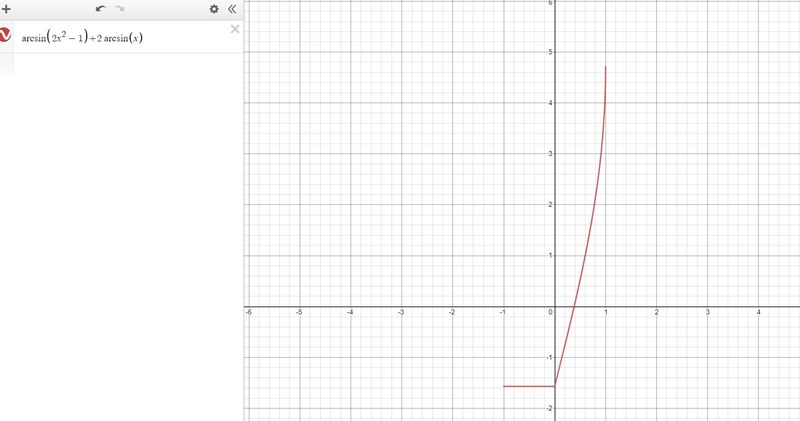
Då ser jag plötsligt att ekvationen satisfieras för alla x mellan -1 och 0. Kan någon förklara mig vart det går fel i min lösningsmetod?
Tack på förhand!
Du gör fel i detta steg:
Detta stämmer inte. Argumentet ska bli . Detta leder om du gör rätt till:
Vilket så klart inte stämmer. Ett annat fel du gör är dubbla vinkeln. Där ska det vara i HL. Hursomhelst, om du gör rätt med din metod kommer du till slut få:
När du får ut vinkeln måste du addera perioder enligt:
Där alltså . Men du vet också att vilket begränsar n.
Ebola skrev:Du gör fel i detta steg:
Detta stämmer inte. Argumentet ska bli . Detta leder om du gör rätt till:
Vilket så klart inte stämmer. Ett annat fel du gör är dubbla vinkeln. Där ska det vara i HL. Hursomhelst, om du gör rätt med din metod kommer du till slut få:
När du får ut vinkeln måste du addera perioder enligt:
Där alltså . Men du vet också att vilket begränsar n.
Okej, då förstår jag! Då får jag efter förenkling i ditt sista steg följande:
Vi har begränsningen att u sträcker sig mellan negativt pi halva och 0, och för varje sådant tal kan vi hitta ett tal n som satisfierar slututtrycket. Detta ger alltså att lösningsmängden blir för alla u inom det givna intervallet, och således blir lösningsmängden för x mellan -1, och 0, precis som i grafen ovan.
Men varför får vi lösningar när vi adderar perioden, men, om vi inte skulle addera perioden, så skulle vi få att u = 0. Jag förstår mig inte på detta.
Om du bara väljer en enda av alla tänkbara möjligheter för mellanresultatet, får du inte fram alla tänkbara lösningar.
Smaragdalena skrev:Om du bara väljer en enda av alla tänkbara möjligheter för mellanresultatet, får du inte fram alla tänkbara lösningar.
Det förstår jag! Jag formulerade mig något dåligt. Det jag inte förstår är att jag får en lösningsmängd där u är beroende av n, och då förstår jag inte riktigt hur jag ska kunna ge en lösning till x utifrån detta.
Vilka värden på n gör att x-värdet hamnar inom definitionsmängden?
Bra att du löste den. Ett annat sätt att övertyga sig själv är att titta på det genom att ta sin(...) på båda sidor och expandera:
Där och . Vi har:
Vi får:
Absolutbeloppen kan hanteras var för sig inom definitionsmängden enligt:
Denna var enkel. Däremot har vi att:
Således får vi två fall i definitionsmängden. Börja med :
Om du dras till minnes att ser vi strax att vi plockat upp en falsk rot på vägen i form . De övriga rötterna och är föga överraskande. Om vi tittar på intervallet istället fås:
Vi ser att för alla i intervallet vilket är vad du hade funderingar kring.
Varför får vi en falsk rot
Därför att definitionsmängden inte stämmer. Om du studerar ursprungsekvationen en stund bör du se att den i själva verket är . Detta för att om är vänsterledet alltid större än . Detta kan motiveras enkelt med enhetscirkeln om du skulle behöva göra det på en tenta.
Ebola skrev:Bra att du löste den. Ett annat sätt att övertyga sig själv är att titta på det genom att ta sin(...) på båda sidor och expandera:
Där och . Vi har:
Vi får:
Absolutbeloppen kan hanteras var för sig inom definitionsmängden enligt:
Denna var enkel. Däremot har vi att:
Således får vi två fall i definitionsmängden. Börja med :
Om du dras till minnes att ser vi strax att vi plockat upp en falsk rot på vägen i form . De övriga rötterna och är föga överraskande. Om vi tittar på intervallet istället fås:
Vi ser att för alla i intervallet vilket är vad du hade funderingar kring.
Varför får vi en falsk rot
Därför att definitionsmängden inte stämmer. Om du studerar ursprungsekvationen en stund bör du se att den i själva verket är . Detta för att om är vänsterledet alltid större än . Detta kan motiveras enkelt med enhetscirkeln om du skulle behöva göra det på en tenta.
Tack så hemskt mycket för ditt svar. Nu har jag sett på 2 olika sätt att lösa problemet på. Om man direkt ser att VL < 0 och då motiverar för att x < 0 så kan man utesluta intervallet x > 0 direkt. På så vis slipper man de falska rötterna, tack för den motiveringen :)



