Trigonometrisk identitet

Sätt HL på gemensamt bråkstreck. Vad kan du skriva om täljaren som?

Menar du såhär.

Jo, det blir ju tan^2x. 

Då är du klar med a)

Ja, b) kan jag inte heller.

Försöker skriva om det så som jag skrev det ovan och landa i sin^2x/cos^2x, och sedan derivera det därifrån kanske 

Här gör jag någonting för att försöka komma någonstans med b)

Glömde kedjeregeln så kommer med en ny bild..

Uppgiften är att du ska derivera höger och vänsterleden var för sig i identiteten

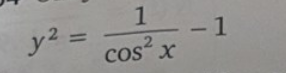
VAd får du om du deriverar högerledet?

vad blir derivatan av y² om du tänker på att y är en funktion av x och du deriverar map x?

Okej.

Det blir 2Y * y'

Jag klarar inte av att härleda derivatan av uttrycket. Eller, ja, jag säger 2tanx + 2tan^2x som jag skrivit då. Sedan dividerat med 2y som är 2tanx.

Så jag får då 1+2tan^2(x)

högerledet 1/cos^2(x) -1 kan vi skriva om som

cos^-2(x) -1 som vi sen deriverar

-2cos^-3(x)*(-sin(x)) = 2sin(x)/cos³(x)

VL har derivatan 2yy'

Alltså

2yy' = 2sin(x)/cos³(x)

dela bägge led med 2y så får vi

y' = sin(x)/(y*cos³(x))

och slutligen sätt in y = tanx = sin/cos och förenkla

Okej, tack